This post introduces basic linear optimizaiton through the example of TopBrass.

TopBrass #

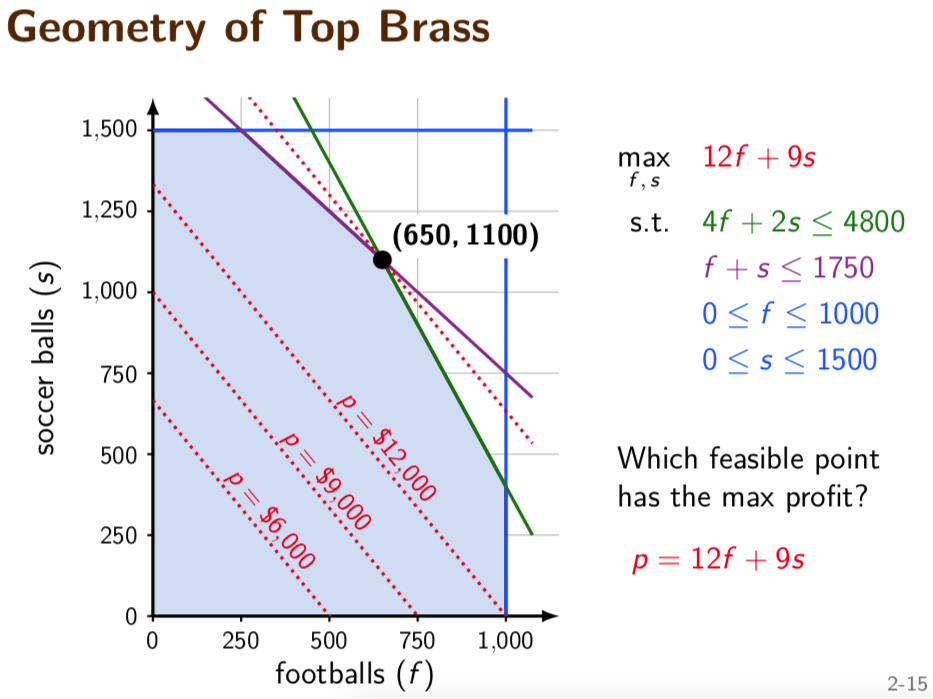
Top Brass Trophy Company makes large championship trophies for youth athletic leagues. At the moment, they are planning production for fall sports: football and soccer. Each football trophy has a wood base, an engraved plaque, a large brass football on top, and returns 12 USD in profit.

Soccer trophies are similar except that a brass soccer ball is on top, and the unit profit is 9 USD.

Since the football has an asymmetric shape, its base requires 4 board feet of wood; the soccer base requires only 2 board feet.

There are 1000 brass footballs in stock, 1500 soccer balls, 1750 plaques, and 4800 board feet of wood. What trophies should be produced from these supplies to maximize total profit assuming that all that are made can be sold?

using HiGHS, JuMP

m = Model(HiGHS.Optimizer)

@variable(m, 0<= f <= 1000)
@variable(m, 0<= s <= 1500)
@objective(m, Max, 12*f + 9*s)
@constraint(m, 4*f + 2*s <= 4800) # board feet of wood
@constraint(m, f + s <= 1750)

$$ f + s \leq 1750.0 $$

print(m)

$$ \begin{aligned} \max\quad & 12 f + 9 s\\ \text{Subject to} \quad & 4 f + 2 s \leq 4800.0\\ & f + s \leq 1750.0\\ & f \geq 0.0\\ & s \geq 0.0\\ & f \leq 1000.0\\ & s \leq 1500.0\\ \end{aligned} $$

println(m)

optimize!(m)

println("The total number of football trophies is ", value(f))
println("The total number of soccer trophies is ", value(s))
println("The highest possible profit is \`$", objective_value(m))

Geometry meaning #

Last modified on 2024-12-07