Optimization: Multi-Period Planning

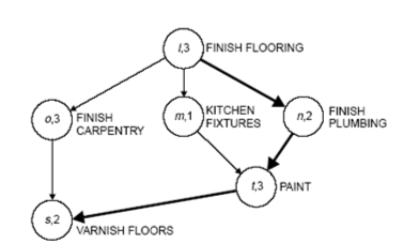
If to complete a project, we need to finish all these tasks, from l to s. The number besides each task indicates the number of days it takes to complete that task. Note that we are allowed to work on multiple tasks simultaneously.

using HiGHS, JuMP, DataStructures

tasks = [:l, :o, :m, :n, :t, :s]
durations = [3, 3, 1, 2, 3, 2]
pre = ([], [:l], [:l], [:l], [:m, :n], [:o, :t])

(Any[], [:l], [:l], [:l], [:m, :n], [:o, :t])

preDict = OrderedDict(zip(tasks, pre))
durDict = OrderedDict(zip(tasks, durations))

OrderedDict{Symbol, Int64} with 6 entries:
  :l => 3
  :o => 3
  :m => 1
  :n => 2
  :t => 3
  :s => 2

The key idea behind the solution is that we set a start time for each task. That start time is at least the start time of any of the preceeding task plus the duration of that preceeding task. Therefore, the start time of task $l$ is zero. We want to minimize the starting time of task $s$.

m = Model(HiGHS.Optimizer)
# initiate start time for each task
@variable(m, tstart[tasks])

# for each task
for t in tasks
    for j in preDict[t]
        # the start time is at least the start time of the preceeding task plus the duration of that 
        # preceeding task
        @constraint(m, tstart[t] >= tstart[j] + durDict[j])
    end
end

# start time for the first task is equal to 0
@constraint(m, tstart[:l] == 0)

# miminize the start time for the last time
@objective(m, Min, tstart[:s] + durDict[:s])

optimize!(m)

Running HiGHS 1.4.2 [date: 1970-01-01, git hash: f797c1ab6]
Copyright (c) 2022 ERGO-Code under MIT licence terms
Presolving model
4 rows, 2 cols, 5 nonzeros
0 rows, 0 cols, 0 nonzeros
Presolve : Reductions: rows 0(-8); columns 0(-6); elements 0(-15) - Reduced to empty
Solving the original LP from the solution after postsolve
Model   status      : Optimal
Objective value     :  1.0000000000e+01
HiGHS run time      :          0.02

objective_value(m)

10.0

Therefore, this project takes at least 10 days.

Last modified on 2023-03-17