配对样本 #
我们首先来看配对样本检测。为了检测一个药物的作用,我们测量了患者服药前的血压 ($X_1$),以及服药后的血压 ($X_2$).
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.stats import t# 此例取自 Chelsey Green 老师教的 STAT 571 at UW-Madison, 2024Fall
X1 = np.array([90, 100, 92, 96, 96, 96, 92, 98, 102, 94, 94, 102, 94, 88, 104])
X2 = np.array([88, 92, 82, 90, 78, 86, 88, 72, 84, 102, 94, 70, 94, 92, 94])
data = {
"Subject": range(1, 16),
"Before (X1)": X1,
"After (X2)": X2
}
# Creating a DataFrame
df = pd.DataFrame(data)
df| Subject | Before (X1) | After (X2) | |
|---|---|---|---|
| 0 | 1 | 90 | 88 |
| 1 | 2 | 100 | 92 |
| 2 | 3 | 92 | 82 |
| 3 | 4 | 96 | 90 |
| 4 | 5 | 96 | 78 |
| 5 | 6 | 96 | 86 |
| 6 | 7 | 92 | 88 |
| 7 | 8 | 98 | 72 |
| 8 | 9 | 102 | 84 |
| 9 | 10 | 94 | 102 |
| 10 | 11 | 94 | 94 |
| 11 | 12 | 102 | 70 |
| 12 | 13 | 94 | 94 |
| 13 | 14 | 88 | 92 |
| 14 | 15 | 104 | 94 |
现在问题来了:请问这个药对于改变病人的血压有效果吗?
上面我们只是对 15 名患者进行实验,现在想象我们对无数患者实验,这些无数患者在服药前血压的均值为 $\mu_1$,标准差为 $\sigma_1$,服药后血压均值为 $\mu_2$,标准差为 $\sigma_2$。我们假设一个群体中所有人的血压分布服从正态分布。
我们假设这款药对于改变病人的血压无效,也即 $H_0: \mu_1 = \mu_2$,$H_A: \mu_1 \ne \mu_2$。
这里有一点没有说明,如果药物无效,那么病人服药前后血压其实是来自一个母体,所以 $\sigma_1 = \sigma2$
我们把患者 $i$ 服药前后血压差记为 $D_i$。
$$D_i = X_{1 i} - X_{2 i}$$
如果 $H_0: \mu_1 = \mu_2$ 成立,那么 $\mathbb{E} (D)$ 该是什么?
如果 $H_0$ 成立,我们知道 $\mu_1 = \mu_2$ 并且 $\sigma_1 = \sigma_2$,那么就相当于从同一个正态分布每次取两个数,算出这两个数的差,重复无数次。
下面我们模拟一下:
def obtain_mean_diff(mean, std_dev, size):
data1 = np.random.normal(mean, std_dev, size)
data2 = np.random.normal(mean, std_dev, size)
mean_diff = np.mean(data1 - data2)
return mean_diff
mean_diffs = []
mean = 100
std_dev = 15
size = 10
for _ in range(100000):
mean_diff = obtain_mean_diff(mean, std_dev, size)
mean_diffs.append(mean_diff)plt.figure(figsize=(6, 4))
plt.hist(mean_diffs, bins="auto", density=False, alpha=0.6, color='g', edgecolor='black')
# Add titles and labels
plt.title(f"Histogram of Mean Differences in Blood Pressue, sample Size = {len(mean_diffs)}, "\
f"μ = {np.mean(mean_diffs):.2f}")
plt.xlabel('Difference in Blood Pressure')
plt.ylabel('Frequency')
plt.show()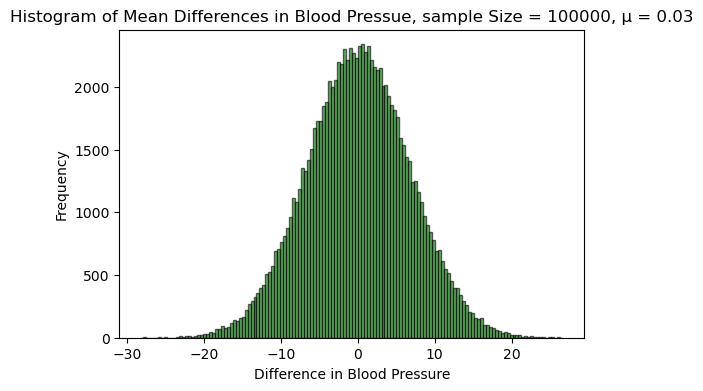 我们看到
我们看到 $\mathbb{E}(D) = 0$,这应该很好理解,即使没有上面的模拟。
回到我们最初的问题:这款药到底有没有效。我们通过上面的模拟,知道了总体 $D$ 是一个均值为 0 的正态分布。若 $H_0$ 成立,则相当于我们从总体 $D$ 中随机抽取了 15 个数(即,15 名患者服药前后血压差)。按照中心极限定理
,这 15 个数的平均值「应该」离 0 不远。具体有多远,我们使用 Z 分数看一下就知道了,但我们并不知道母体 $D$ 的标准差为何,所以只能用样本标准差来估计,这就转换成了一个很典型的单样本 T 检验问题,我们之前讲过
。
$$t = \frac{\bar{D} - \mathbb{E}(D)}{\frac{S_D}{\sqrt{15}}}$$
d = X1 - X2
d_bar = np.mean(d)
s_d = np.std(d, ddof=1)
t_value = d_bar / (s_d/np.sqrt(len(X1)))
df = len(X1) - 1
p_value = 2*(1 - t.cdf(abs(t_value), df = df))
p_value$p$ 值 小于 0.01。这表示如果 $H_0$ 成立,那么我们观测到 $X_1$ 和 $X_2$ 这次结果的概率小于 0.01,所以我们有理由拒绝这个陈述:该药物无效。
换成人话就是,如果该药物无效,这次实验结果出现的概率很低。所以我们拒绝承认该药物无效这个说法。
独立样本 #
方差相等 #
看完配对样本,我们再来看一下独立样本。
为了检测一款药物的疗效,我们让第一组 15 名患者服用该药物并测量了血压 ($X_1$),让第二组 10 名患者服用安慰剂并测量了血压 ($X_2$)。
X1 = np.array([90, 100, 92, 96, 96, 96, 92, 98, 102, 94, 94, 102, 94, 88, 104])
X2 = np.array([88, 92, 82, 90, 78, 86, 88, 72, 84, 102])请问:该药物对于改变病人血压是否有效?
这次的观察结果和配对样本的不同在于,在这次的独立样本中,我们无法使用 $D_i = X_{1 i} - X_{2 i}$ 这个概念,因为并不存在两两对应的这一情况。
上面我们只是对 15 名和 10 名患者进行实验,现在想象有无数的患者服用该药物后的血压的均值为 $\mu_1$,标准差为 $\sigma_1$。有无数的患者服用安慰剂后的血压均值为 $\mu_2$,标准差为 $\sigma_2$。
我们把上面这句话换成更专业的语言。
有两组独立样本:
样本 $X_1$:$X_1, X_2 ... X_{n_1}$ 来自总体 $\mathcal{N} (\mu_1, \sigma_1)$
样本 $X_2$:$Y_1, Y_2 ... Y_{n_2}$ 来自总体 $\mathcal{N} (\mu_2, \sigma_2)$
我们假设服用该药物的母体和服用安慰剂的母体,血压标准差一样,也就是说 $\sigma_1 = \sigma_2 = \sigma$。
根据中心极限定理 ,我们知道
$$\bar{X_1} \sim \mathcal{N}\left(\mu_1, \frac{\sigma^2}{n_1} \right)$$
$$\bar{X_2} \sim \mathcal{N}\left(\mu_2, \frac{\sigma^2}{n_2} \right)$$
我们进一步知道:
$$\bar{X_1} - \bar{X_2} \sim \mathcal{N}\left(\mu_1 - \mu_2, \frac{\sigma^2}{n_1} + \frac{\sigma^2}{n_2}\right)$$
这一点我现在懒得证明,感兴趣的朋友自己用代码模拟一下就知道了。
我们假设这款药对于改变病人的血压无效,也即 $H_0: \mu_1 = \mu_2$,$H_A: \mu_1 \ne \mu_2$。
所以
$$\bar{X_1} - \bar{X_2} \sim \mathcal{N}\left(0, \frac{\sigma^2}{n_1} + \frac{\sigma^2}{n_2}\right)$$
转换成 $Z$ 分数:
$$Z = \frac{\bar{X_1} - \bar{X_2}}{\sigma \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim \mathcal{N}(0, 1)$$
$t$ 分布的含义是说,在 $Z$ 分布中,当我们用样本方差来估计总体方差时,得出来的 $Z$ 服从 $t$ 分布。现在的问题是,如何得到样本方差。
我们知道样本 1 和样本 2 的方差分别为:
$$s_1^2 = \frac{1}{n_1 - 1}\sum_{i = 1}^{n_1}\left(X_{i} - \bar{X_1}\right)$$
$$s_2^2 = \frac{1}{n_2 - 1}\sum_{i = 1}^{n_2}\left(Y_{i} - \bar{X_2}\right)$$
我们这样计算 $X_1 - X_2$ 的方差:
$$S_p^2 = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}$$
把 $\sigma$ 和 $S_p$ 对调一下,我们现在想证明的是:
$$\frac{\bar{X_1} - \bar{X_2}}{S_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t_{n_1 + n_2 - 2}$$
那我们来证明一下。
首先,根据卡方分布的知识 ,我们知道
$$\frac{(n_1 - 1)s_1^2}{\sigma^2} \sim \chi_{n_1 - 1}^2$$
$$\frac{(n_2 - 1)s_2^2}{\sigma^2} \sim \chi_{n_2 - 1}^2$$
卡方分布有一个性质:如果两个独立随机变量的分布服从卡方分布,那么这两个随机变量之和也服从卡方分布,且自由度是这两个卡方分布自由度之和。所以
$$\frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{\sigma^2} \sim \chi_{n_1 + n_2 - 2}^2$$
所以
$$S_p^2 \sim \frac{\sigma^2}{n_1 + n_2 - 2} \chi_{n_1 + n_2 - 2}^2$$
所以
$$S_p = \sigma \sqrt{\frac{\chi_{n_1 + n_2 - 2}^2}{n_1 + n_2 - 2}}$$
我们把上面这个公式以及
$$\bar{X_1} - \bar{X_2} = Z \cdot \sigma \cdot \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}$$
代入
$$\frac{\bar{X_1} - \bar{X_2}}{S_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}$$
得到
$$\frac{\bar{X_1} - \bar{X_2}}{S_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} = \frac{Z}{\sqrt{\frac{\chi_{n_1 + n_2 - 2}^2}{n_1 + n_2 - 2}}}$$
这个结果和我们在 t 分布 讲的一样,所以
$$\frac{\bar{X_1} - \bar{X_2}}{S_p \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t_{n_1 + n_2 - 2}$$
得证。
方差不等 #
同样的问题,如果我们无法确定两个总体的方差相等,那么
$$\bar{X_1} - \bar{X_2} \sim \mathcal{N}\left(\mu_1 - \mu_2, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\right)$$
若 $H_0$ 成立:
$$\bar{X_1} - \bar{X_2} \sim \mathcal{N}\left(0, \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}\right)$$
所以
$$T = \frac{\bar{X_1} - \bar{X_2}}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}$$
这样算出来的 $T$ 并不符合 $t_{n_1 + n_2 - 2}$。统计量 $T$ 只是近似服从 t 分布,自由度计算方法如下:
$$\frac{\left(\frac{s_1^2}{n_1} + \frac{s_2^2}{n_1}\right)^2}{\frac{1}{n_1 - 1}\left(\frac{s_1^2}{n_1}\right)^2 + \frac{1}{n_2 - 1}\left(\frac{s_2^2}{n_2}\right)^2}$$
这被称为 Welch’s t test 。
#统计学最后一次修改于 2025-06-25 • 编辑本页