我学习统计学比较喜欢的方法是：
- 问题为先导
- 用频率，不用密度
- 模拟为先，如有必要再继续用数学公式（如无必要则只用模拟）
这篇主要讲标准误 (standard error) 和中心极限定理 (Central Limit Theorem)。我说了以问题为先导，那我们先来看一个问题：
全球人类的智商分布符合正态分布，
$\mathcal{N}(100, 15^2)$。我们从全球 80 亿人中随机抽取 100 个人，这 100 人的平均智商大于等于$110$的概率是多少？
标准误 #
如果我们只用模拟，不用数学公式。上面这题就很好解决：80 亿人抽 100 个人，我们重复 1 万次，每次都算出平均值。平均值大于等于 110 的次数除以 1 万，就是随机抽取 100 人，该 100 人平均智商大于等于 110 的概率。这个应该很好理解吧？
但我们不满足于此。我们想看看从正态分布为 $\mathcal{N}(\mu, \sigma^2)$ 的母体中随机抽取 $M$ 个大小为 $N$ 的样本。每个样本算出其平均值 ($\bar{X}$)，也就是说总共有 $M$ 个 $\bar{X}$。我们想看一下 $\bar{X}$ 的分布是否存在某种规律。顺带提一句：这个分布的标准差被称为「标准误 (standard error)」。
我们先把母体的正态分布模拟一下：
import numpy as np
import matplotlib.pyplot as plt
# Set the seed for reproducibility
np.random.seed(42)
# Parameters for the normal distribution
mean = 100 # Mean of the distribution
std_dev = 15 # Standard deviation of the distribution
size = 100000 # Number of data points
# Generate the data
data = np.random.normal(mean, std_dev, size)
population_mu = np.mean(data)
population_sigma = np.std(data)
# Create a histogram of the data
plt.figure(figsize=(6, 4))
plt.hist(data, bins="auto", density=False, alpha=0.6, color='g', edgecolor='black')
# Add titles and labels
plt.title(f"Histogram of IQ Distribution, sample Size = {size}, "\
f"μ = {population_mu:.2f}, σ = {population_sigma:.2f}")
plt.xlabel('IQ')
plt.ylabel('# of People')
# Show the plot
plt.show()
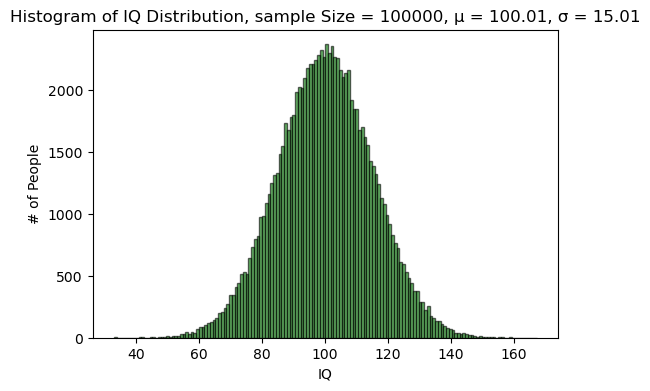然后我们从母体中抽取 num_sample 个大小为 sample_size 的样本，得到每个样本的平均值：
def obtain_sample_means(data, sample_size, num_samples):
"""sample from data, each time to get a sample of sample_size
and calcuate the sample's mean.
Continue for num_samples times.
"""
sample_means = np.zeros(num_samples)
for i in range(num_samples):
sample = np.random.choice(data, size=sample_size, replace=False)
sample_means[i] = np.mean(sample)
return sample_means
num_samples = 2000
sample_sizes = [10, 100, 1000, 10000]
sample_means = {size: obtain_sample_means(
data, size, num_samples) for size in sample_sizes}
sample_means['num_samples'] = num_samples
# Plotting
plt.figure(figsize=(12, 10))
# Create subplots
for i, size in enumerate(sample_sizes):
sub_data = sample_means[size]
mu = np.mean(sub_data)
sigma = np.std(sub_data)
plt.subplot(2, 2, i + 1) # 2x2 grid, subplot index starts at 1
plt.hist(sub_data, bins="auto", density=False,
alpha=0.7, color='steelblue', edgecolor='black')
# Plot vertical line at the mean
plt.axvline(mu, color='red', linestyle='--', linewidth=2)
plt.title(rf'Sample Size = {size}, $\mathbb{{E}}[\bar{{X}}] = {mu:.2f}$, $S = {sigma:.2f}$')
plt.xlabel('$\\bar{{X}}$')
plt.ylabel('# of Samples')
# Adjust layout
plt.tight_layout()
# Show the plot
plt.show()
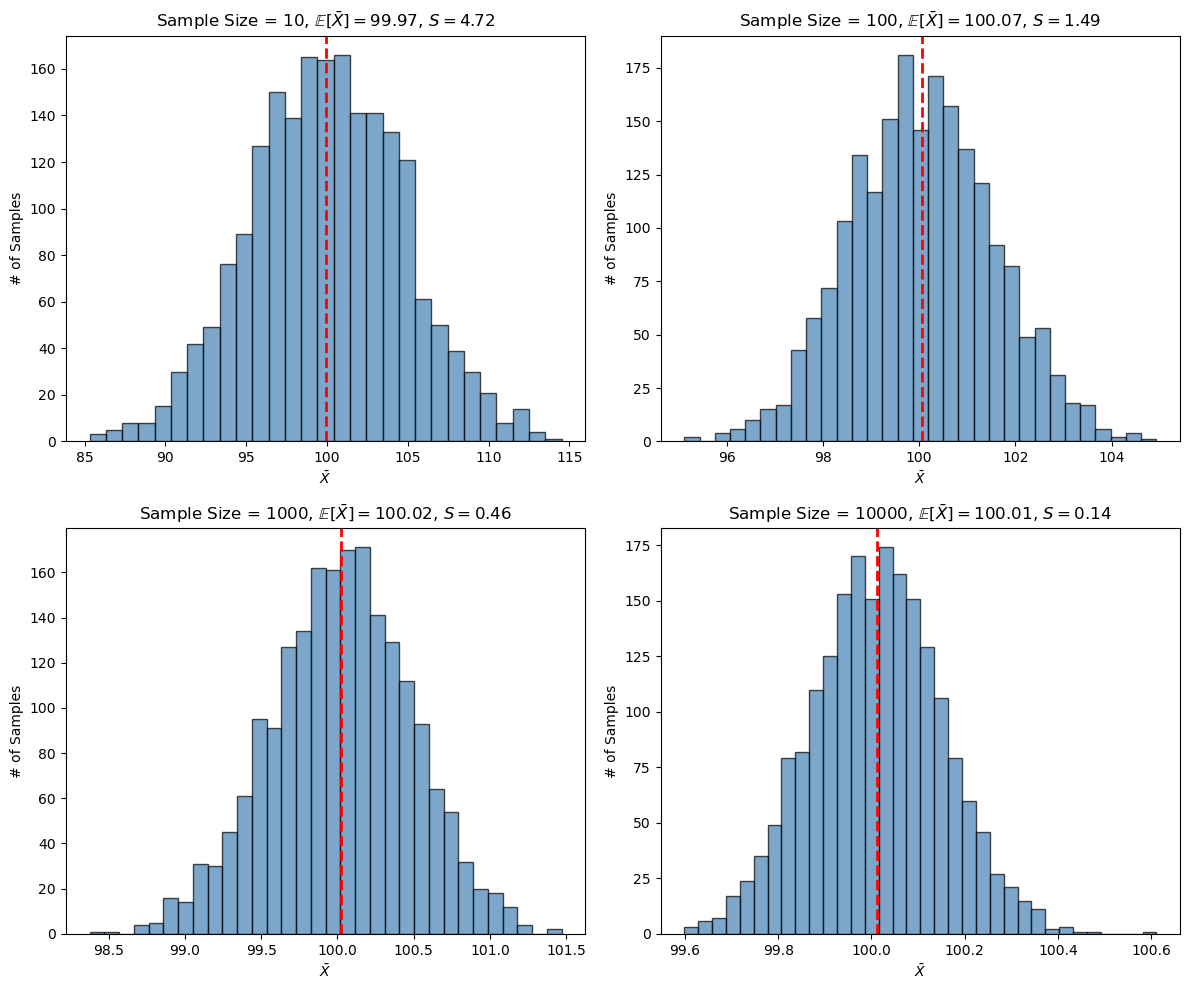我们直观可以感受到的是，不管样本大小为何，$\bar{X}$ 的平均值不变，和母体一样。但是随着样本大小逐渐增大，$\bar{X}$ 的标准差变得越来越小。
下面，我们具体算一下：
print(f"μ = {population_mu:.2f}, σ = {population_sigma:.2f}")
for sample_size in sample_sizes:
sub_data = sample_means[sample_size]
mu = np.mean(sub_data)
sigma = np.std(sub_data)
print(f"N = {sample_size}, 样本平均值的平均值 = {mu:.2f}, 样本平均值的标准差 = {sigma:.2f}, " \
f"σ/sqrt({sample_size}) = {(population_sigma/np.sqrt(sample_size)):.2f}")
从一个正态分布 $\mathcal{N}(\mu, \sigma^2)$ 的母体中，随机不放回抽取 $M$ 个大小为 $N$ 的样本，样本的平均值 $\bar{X}$ 的分布为：
$$ \bar{X} \sim \mathcal{N} \left( \mu, \frac{\sigma^2}{N} \right) $$
解答问题 #
有了以上结论，最初的问题就很好解答了。
全球人类的智商分布符合正态分布，
$\mathcal{N}(100, 15^2)$。我们从全球 80 亿人中随机抽取 100 个人，这 100 人的平均智商大于等于$110$的概率是多少？
从 80 亿人中抽取 100 人，假设我们抽取无数次，每次算出这 100 人的智商平均值 ($\bar{X}$)。$\bar{X}$ 的分布为：
$$\bar{X} \sim \mathcal{N} \left(100, \frac{15^2}{100} \right)$$
$\bar{X} = 100$ 对的 $Z$ 值为 $\frac{110 - 100}{1.5} = \frac{20}{3}$
import scipy.stats as stats
z = 20/3
prob_less_equal = stats.norm.cdf(z)
prob_greater_equal = 1 - prob_less_equal
print(f"P(Z ≥ {z:.2f}) = {prob_greater_equal:.4f}")
中心极限定理 #
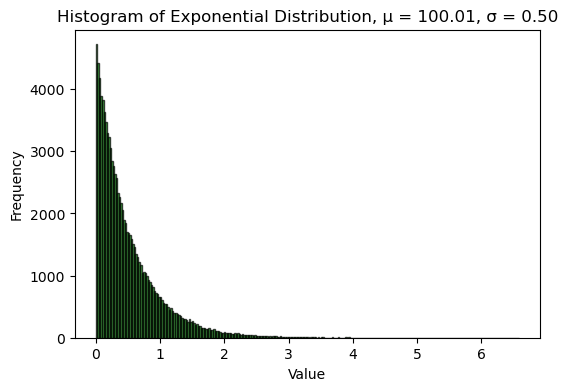
上面我们是从正态分布的母体中抽样。假如我们从非正态分布的母体中抽样，每次也算出样本平均值，这些样本平均值的分布会怎么样？
labmda_param = 2.0
sample_size = 100000
data = np.random.exponential(1/labmda_param, sample_size)
pupulation_mu = np.mean(data)
population_sigma = np.std(data)
plt.figure(figsize=(6,4))
plt.hist(data, bins = "auto", density=False,
alpha = 0.7, color='green',
edgecolor='black')
plt.title(f"Histogram of Exponential Distribution, "\
f"μ = {population_mu:.2f}, σ = {population_sigma:.2f}")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.show()
num_samples = 2000
sample_sizes = [10, 100, 1000, 10000]
sample_means = {size: obtain_sample_means(
data, size, num_samples) for size in sample_sizes}
# Plotting
plt.figure(figsize=(12, 10))
# Create subplots
for i, size in enumerate(sample_sizes):
sub_data = sample_means[size]
mu = np.mean(sub_data)
sigma = np.std(sub_data)
plt.subplot(2, 2, i + 1) # 2x2 grid, subplot index starts at 1
plt.hist(sub_data, bins="auto", density=False,
alpha=0.7, color='steelblue', edgecolor='black')
# Plot vertical line at the mean
plt.axvline(mu, color='red', linestyle='--', linewidth=2)
plt.title(rf'Sample Size = {size}, '
rf'$\mathbb{{E}}[\bar{{X}}] = {mu:.2f}$, '
rf'$S = {sigma:.2f}$')
plt.xlabel('$\\bar{{X}}$')
plt.ylabel('# of Samples')
# Adjust layout
plt.tight_layout()
# Show the plot
plt.show()
print(f"μ = {population_mu:.2f}, σ = {population_sigma:.2f}")
for sample_size in sample_sizes:
sub_data = sample_means[sample_size]
mu = np.mean(sub_data)
sigma = np.std(sub_data)
print(f"N = {sample_size}, Mean (X̄) = {mu:.2f}, Std (X̄) = {sigma:.4f}, " \
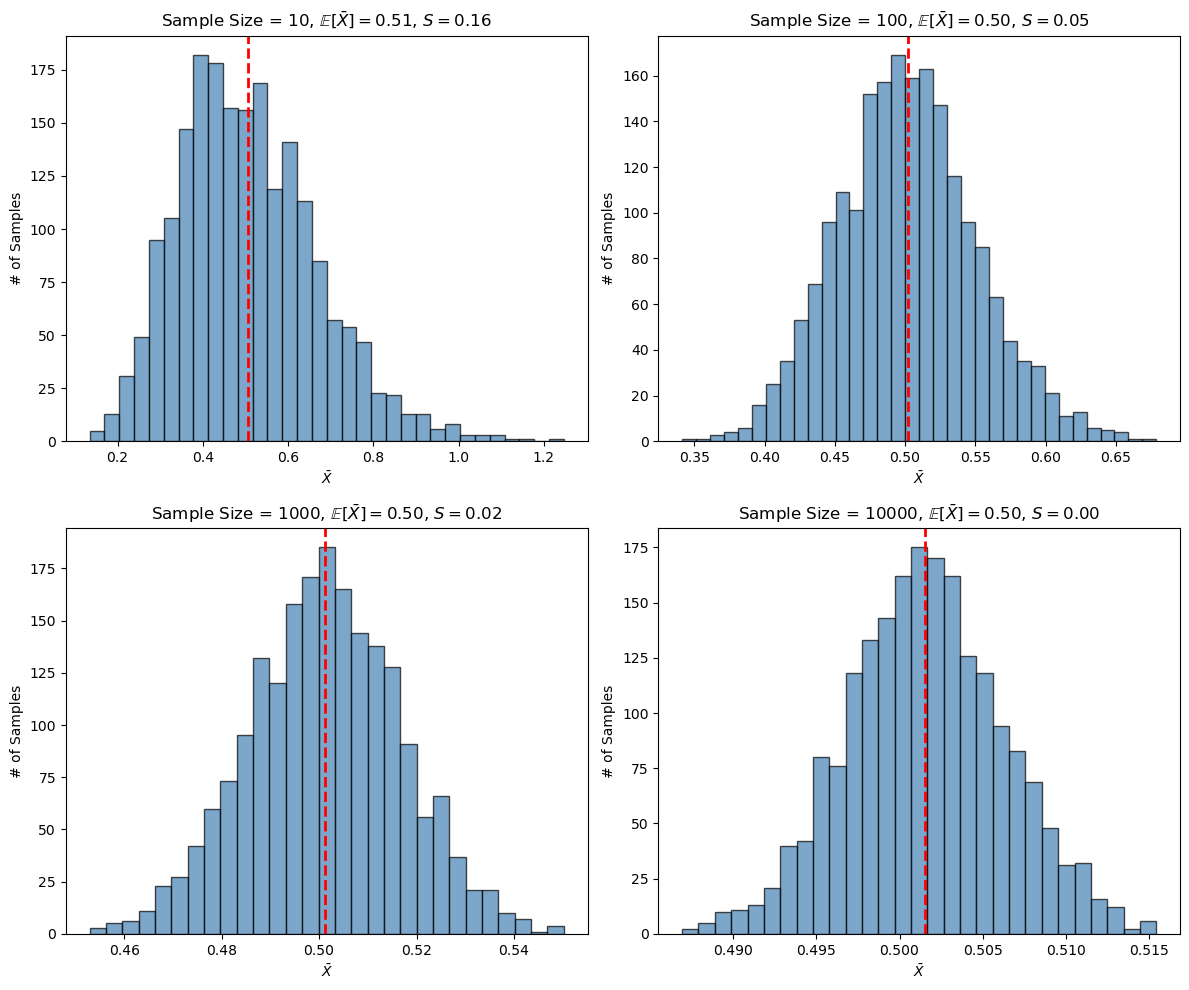
f"σ/sqrt({sample_size}) = {(population_sigma/np.sqrt(sample_size)):.4f}")
$N \ge 30$ 即可)，$\bar{X}$ 的分布都无限趋近于正态分布。
结论是，不论母体分布是不是正态，假设母体平均值为 $\mu$，标准差为 $\sigma$，我们从母体中随机不放回抽取 $M$ 个大小为 $N$ 的样本，样本的平均值 $\bar{X}$ 的分布为：
$$ \bar{X} \sim \mathcal{N} \left( \mu, \frac{\sigma^2}{N} \right) $$
以上就是中心极限定理。至于「每次样本的样本量足够大」到底是多大，我们从上图中看到，如果母体是一个高度偏态分布，那么当 $N$ 大于 $1000$ 时，$\bar{X}$ 的分布就已经呈现正态分布的形态了。
但是在具体用的时候，我们还是要遵循一定的法则。
- 如果母体本身是正态分布，那么对于
$N \ge 1$，$\bar{X}$的分布理论上完全符合上面所描述的正态分布。 - 如果母体本身非正态分布，对于
$N \ge 30$，$\bar{X}$的分布基本上也符合上述正态分布的特征。 - 如果母体本身非正态分布，对于
$N \lt 30$，$\bar{X}$的分布无法用上面的正态分布准确描述。此时，较好的做法是使用$t$分布（$t$-distribution）来进行估计。
最后一次修改于 2024-12-07