PID controller #
PID is short for “Proportional-Integral-Derivative”. What it does is that if you have a planned trajectory for a vehicle which is now at a specific location and have a specific initial speed, PID will allow this vehicle to get to the planned trajectory. You accomplish this through PID by tweaking the three parameters:
$k_P$$k_I$$k_D$
If you multiply $k_P$ by the distance between the planned location and the actual location at any timestamp, you get $a_P$. If you multiply $k_I$ by the difference between the integral of the planned location and that of the actual location at any timestamp, you get $a_I$. If you multiply $k_D$ by the speed difference between the planned trajectory and the actual vehicle at any timestamp, you get $a_D$.
If you add up $a_P$, $a_I$, and $a_D$, you get $a$, which is the acceleration for the actual vehicle.
PID for constant speed #
The planned trajectory starts from location 0 at time 0. It is cruising at 30m/s speed for 50 seconds.The actual location is 3 at time 0 and the actual speed is 28m/s at time 0.
using Plots, Distributions, Random
function get_data(t, k_p=2, k_i=0, k_d=1)
# initial state
# y for the planned vehicle, x for the actual vehicle
y = 0 # position
int_y = 0 # integral of position
y_dot = 30 # speed
x = 3
int_x = 0
x_dot = 28
a_p = k_p * (y - x)
a_i = k_i * (int_y - int_x)
a_d = k_d * (y_dot - x_dot)
a = a_p + a_i + a_d
# if time is 0, return the initial state
if t == 0
return (y, x)
else
for i in time_delta:time_delta:t
# 0.2, 0.4, 0.6, ...
x_dot_prev = x_dot
x_dot += a * time_delta
# THIS IS USING APPROXIMATION!
x += 0.5*(x_dot_prev + x_dot) * time_delta
int_x += x * time_delta
# update y
y_dot = y_dot # constant speed at all time
y += y_dot * time_delta
int_y += y * time_delta
# update a_p, a_i, a_d, and a for usage at next timestamp
a_p = k_p * (y - x)
a_i = k_i * (int_y - int_x)
a_d = k_d * (y_dot - x_dot)
a = a_p + a_i + a_d
end
return (y, x)
end
end
get_data (generic function with 5 methods)
time_delta = 0.2
time_span = 0.0:time_delta:50
0.0:0.2:50.0
function make_plot(data, title, label, xlabel, ylabel)
Plots.plot(time_span, data,
title=title,
label=label,
linewidth=0.5,
markershape = :auto,
markersize = 2,
linestyle = :auto,
mc= :auto,
xlabel = xlabel,
ylabel = ylabel,
legend=:bottom
)
end
make_plot (generic function with 1 method)
ys = [get_data(i, 2, 0, 1)[1] for i in time_span]
xs = [get_data(i, 2, 0, 1)[2] for i in time_span]
251-element Vector{Real}:
3
8.52
13.915199999999999
19.253951999999998
24.59818752
29.999490355200003
35.496625508352004
41.114488996331524
46.8643352065278
52.745059206570446
58.74526263008063
64.84581249542273
71.02260938267628
⋮
1434.0000000008072
1440.0000000013742
1446.0000000017405
1452.000000001909
1458.000000001898
1464.0000000017367
1470.0000000014622
1476.0000000011148
1482.0000000007337
1488.000000000355
1494.0000000000084
1499.9999999997167
make_plot(
[ys, xs],
"planned and actual",
["planned" "actual"],
"time",
"planned and actual"
)
savefig("/en/blog/2023-02-28-pid_files/pid-01.png")

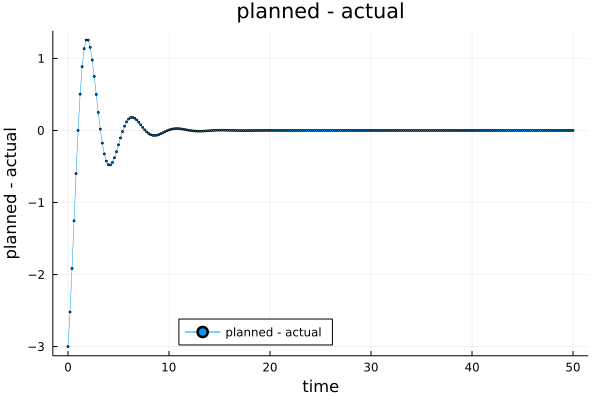
make_plot(
ys-xs,
"planned - actual",
"planned - actual",
"time",
"planned - actual"
)
savefig("/en/blog/2023-02-28-pid_files/pid-02.png")
Dynamic speed (with random noise) #
The planned trajectory starts from location 0 at time 0. It is cruising at 30m/s speed for the first 10 seconds, then decreasing to 10 m/s with deceleration
$-2𝑚/𝑠^2$for 10 seconds and then accelerating to 30m/s with acceleration$2𝑚/𝑠^2$for 10 seconds, and then cruising at 30 m/s for 20 seconds.
The actual location is 3 at time 0 and the actual speed is 28m/s at time 0.
Assuming the acceleration cannot be precisely controlled, and always has a random error uniformly distributed over
$[-0.2, 0.2] m/s$
function get_y_dot(t)
"""This function gets the speed of the planned vehicle
"""
if t <= 10
y_dot = 30
elseif t <= 20
y_dot = 30
for i in 10+time_delta:time_delta:t
y_dot += time_delta*(-2)
end
elseif t <= 30
y_dot = 10
for i in 20+time_delta:time_delta:t
y_dot += time_delta*2
end
else
y_dot = 30
end
return y_dot
end
get_y_dot (generic function with 1 method)
Tesing the function of get_y_dot:
get_y_dot(15)
20.000000000000036
get_y_dot(22)
14.000000000000004
function get_data(t, k_p=2, k_i=0, k_d=1, noise = true)
"""This function returns the trajectory of the planned vehicle (y)
and the actual vehicle (x)
The key is that the initial acceleration of the actual vehicle can be calculated
through the initial state and the set parameters. Using this acceleration at t=0,
we can calculate the velocity of the actual vehicle at the next timestamp. Then,
using x_dot, we can calculate x and int_x.
y_dot, y, and the int_y can be calculated easily.
"""
# initial state
# y for the planned vehicle, x for the actual vehicle
y = 0 # position
int_y = 0 # integral of position
y_dot = 30 # speed
x = 3
int_x = 0
x_dot = 28
a_p = k_p * (y - x)
a_i = k_i * (int_y - int_x)
a_d = k_d * (y_dot - x_dot)
if noise
a = a_p + a_i + a_d + rand(Uniform(-0.2, 0.2))
else
a = a_p + a_i + a_d
end
if t == 0
return (y, x)
else
for i in time_delta:time_delta:t
x_dot_prev = x_dot
x_dot += a * time_delta
# THIS IS USING APPROXIMATION!
x += 0.5*(x_dot_prev + x_dot) * time_delta
int_x += x * time_delta
# update y
y_dot = get_y_dot(i)
y += y_dot * time_delta
int_y += y * time_delta
# update a_p, a_i, a_d, and a for usage at next timestamp
a_p = k_p * (y - x)
a_i = k_i * (int_y - int_x)
a_d = k_d * (y_dot - x_dot)
if noise
a = a_p + a_i + a_d + rand(Uniform(-0.2, 0.2))
else
a = a_p + a_i + a_d
end
end
return (y, x)
end
end
get_data (generic function with 5 methods)
ys = [get_data(i, 2, 0, 1)[1] for i in time_span]
xs = [get_data(i, 2, 0, 1)[2] for i in time_span]
251-element Vector{Real}:
3
8.518715767262622
13.906232802166503
19.268572854391913
24.6096425130715
30.02599498962064
35.45927678410515
41.09226062787909
46.86326171393311
52.7531619121299
58.74007729213587
64.88326196481631
71.03580647914927
⋮
1233.9981479653238
1240.010372398277
1246.0066976688347
1252.0239301638433
1258.0021171428577
1264.008764132957
1270.021276479265
1275.9923591224674
1282.033955662245
1288.014337231835
1293.9907637632514
1299.9826222077306
make_plot(
[ys, xs],
"planned and actual",
["planned" "actual"],
"time",
"planned and actual"
)
savefig("/en/blog/2023-02-28-pid_files/pid-03.png")

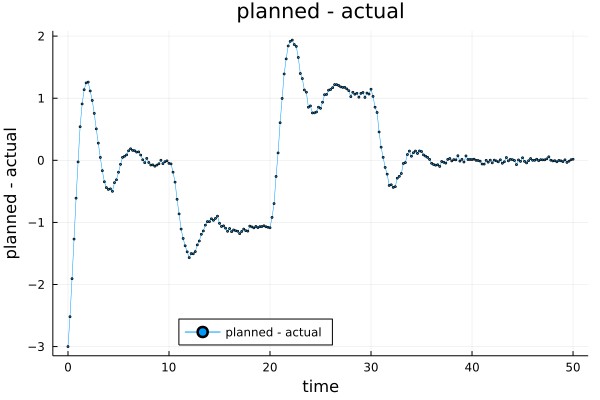
make_plot(
ys-xs,
"planned - actual",
"planned - actual",
"time",
"planned - actual"
)
savefig("/en/blog/2023-02-28-pid_files/pid-04.png")
Questions #
- In pid, the x/y_dot, and int_y/x is using approximation, can we get the exact form?
It’s very difficult to get the analytical form.
- How to get the optimal value
It’s also very difficult. It involves non-linear programming.
#self-drivingLast modified on 2025-05-06