概念讲解 #
无限高斯混合模型 (Infinite Gaussian Mixture Model, IGMM) 是 高斯混合模型 的延伸。它处理这样的情况:我们不知道有几个簇 (cluster) 。
这时候大体上有两种解决办法。第一种是测试不同的簇数,然后比较哪个结果好,常用的方法有 Elbow method (使用 Sum of Squared Errors)、Akaike information criterion 、Bayesian information criterion 等。
第二种方法,也是我们这篇要讲的,假设有无数个簇。设数据点 $x_i$ 所属的簇为 $z_i = k$。其中 $k$ 表示一个具体的簇。我们假设每个簇的数据符合正态分布,$\mathcal{N}(\mu_k, \sigma_k^2)$。那我们最后想得到的是两个概率分布:
- 对于一个数据点
$x_i$,我们想知道该数据点属于某一个簇的概率,$P(z_i = k|x_i)$,这是一个离散分布。 - 已知某一簇所包含的数据点集合
$X_k = \{x_i|z_i = k\}$,我们想知道该簇参数的后验分布,即不同$\mu_k$与$\sigma_k^2$的概率分布,$P(\mu_k, \sigma_k^2|X_k)$,这是一个连续分布。
看到这里,你可能会问:(1) 我说了一个数据点属于某一簇只是一个概率事件,只要不是 100%,那我们就不知道它到底属于哪个簇。既然如此,我们如何知道 $X_k = \{x_i|z_i = k\}$? (2) 簇参数是一个分布,并不是具体的值,那如何算 $P(z_i = k|x_i)$? 如果你能问出这两个问题,我只能说你太牛逼了。先别急,接着往下看。
为了计算这两个概率,我们需要拿出「贝叶斯公式」这个杀手锏:
\begin{equation} P(z_i = k|x_i) \propto P(z_i = k) \cdot P(x_i|z_i = k) = P(z_i = k) \cdot P(x_i|\mu_k, \sigma_k^2) \tag{1} \end{equation}
\begin{equation} P(\mu_k, \sigma_k^2|X_k) \propto P(\mu_k, \sigma_k^2) \cdot \prod_{x_i \in X_k} P(x_i|\mu_k, \sigma_k^2)\tag{2} \end{equation}
对于公式 (1):
$ P(z_i = k)$ 是簇的先验概率。也就是说,我们在没有任何信息的情况下,如何推断一个数据点 $x_i$ 属于哪个簇。
$P(x_i|z_i = k)$ 表示在 $x_i$ 属于簇 $k$ 的条件下,数据点的似然 (Likelihood,你可以理解为「可能性」)。对于高斯分布,这个似然概率就是横坐标某一个 $x$ 所对应的密度值 (PDF)。也就是说,$P(x_i|z_i = k) = P(x_i|\mu_k, \sigma_k^2)$
对于公式 (2):
最后我们想得到的 $P(\mu_k, \sigma_k^2|X_k)$ 是关于给定 $X_k$ 这条信息后,我们对于该簇参数的认识。那我们选择什么分布来描述我们对参数的认识呢?
我们先看簇均值 $\mu_k$,可选的分布很多,比如正态分布、 T 分布、拉普拉斯分布等。$\sigma_k^2$ 的话,我们要确保 $\sigma_k^2 \ge 0$,可选的分布也有很多,比如伽马分布、逆伽马分布、卡方分布、对数正态分布、指数分布等。都可以保证结果(分布的随机变量)非负。
另外,我们需要注意的是,$P(\mu_k, \sigma_k^2|X_k)$ 是一个联合概率,因为 $\mu_k$ 与 $\sigma_k^2$ 是关联的。当 $\sigma_k^2$ 比较小时,我们对均值的不确定性就比较小。因此,后验分布也需要描述它们的关系。
$\prod_{x_i \in X_k} P(x_i|\mu_k, \sigma_k^2)$ 是将多个正态分布密度函数相乘。但是在具体计算时,我们是逐点计算:
\begin{equation} P(\mu_k, \sigma_k^2|x_i, z_i = k) \propto P(\mu_k, \sigma_k^2) \cdot P(x_i|\mu_k, \sigma_k^2)\tag{3} \end{equation}
对 $X_k$ 中的所有点算一遍,最后的结果就是 $P(\mu_k, \sigma_k^2|X_k)$
这里为什么逐点计算的结果和连乘的结果一样?设想,对于集合 $X_k$ 中第一个数据点,$P(\mu_k, \sigma_k^2) \cdot P(x_1|\mu_k, \sigma_k^2)$ 得到的后验是计算 $x_2$ 时的先验。所以逐点计算和该簇所有点一起计算,结果是一样的。
现在的问题是,我们如何选择均值和方差的分布,以满足上面的两个个要求:(1) 符合实际。也就是从上面列出的可选分布中选。(2) 是一个联合概率。另外,最好符合第三个要求 (3)计算方便。
科学家发现一个很巧的事情:如果先验概率我们选择用正态分布描述均值,用逆伽马分布描述方差,那么和 $\prod_{x_i \in X_k} P(x_i|\mu_k, \sigma_k^2)$ 相乘之后,最后得到的分布和先验分布形式相同,也是「正态-逆伽马分布」 (Normal-Inverse-Gamma Distribution
)。这就大大简化了计算量,所以我们选择用正态分布描述均值,用逆伽马分布描述方差。其中,数据决定逆伽马函数,而逆伽马函数决定了正态分布。这样一来,上面的三个要求全都满足了。
更多这种很巧的案例可以参考「共轭先验 」。
具体的计算过程 #
我们来讲一下具体怎么计算。我们是逐点计算的,也就是对每一个数据点进行遍历。
公式 (3) #
我们先来看公式 (3)。
假设当前的先验 $P(\mu_k, \sigma_k^2)$ 是正态-逆伽马分布:
$$\sigma^2 \sim \text{InvGamma}(\alpha_0, \beta_0)$$
$$\mu|\sigma^2 \sim \mathcal{N}(\mu_0, \frac{\sigma^2}{\kappa_0})$$
其中:
$\alpha_0, \beta_0$:控制方差分布的形状$\mu_0$:均值的先验均值$\kappa_0$:对均值先验的确信程度
属于某簇 $k$ 的一个新数据点 $x_i$ 的似然函数:
$$P(x_i|\mu_k, \sigma_k^2) = \frac{1}{\sqrt{2\pi\sigma_k^2}}\exp\left( -\frac{(x_i - \mu_k)^2}{2\sigma_k^2} \right)$$
需要注意的是,$\mu_k$ 和 $\sigma_k^2$ 是该簇参数当前的后验分布,即 $P(\mu_k, \sigma_k^2|X_k)$。也就是说,它们本身也是一个分布,而不是一个确定的值。对于该簇的「第一个」数据点,$\mu_k$ 和 $\sigma_k^2$ 就是先验分布。
$\mu_k$ 和 $\sigma_k^2$ 是分布,而非具体的值,但是 $P(x_i|\mu_k, \sigma_k^2)$ 确确实实是一个具体的值,怎么办?我们需要考虑所有的 $\mu$ 和 $\sigma^2$,然后取加权平均。权重就是每个 $\mu$ 和 $\sigma^2$ 在$P(\mu_k, \sigma_k^2|X_k)$ 中的密度值:
$$P(x_i|\mu_k, \sigma_k^2) = \int_{\mu} \int_{\sigma^2} P(x_i|\mu, \sigma^2) \cdot P(\mu, \sigma^2|X_k) \cdot d\mu \cdot d\sigma^2 \tag{4}$$
根据公式 (3),这个双重积分还要在乘上 $P(\mu_k, \sigma_k^2)$ 这个先验分布,那真是「难算他妈给难算开门,难算到家了」。
不过好在数学家已经提前算好了:如果 $P(\mu_k, \sigma_k^2)$ 用正态-逆伽马分布的话,带入上面的公式,得到的结果依然是一个正态-逆伽马分布,这就是「共轭先验」。
这样一来,我们直接根据这些先辈得出的「共轭先验」的性质就可以更新正态-逆伽马分布的参数:
$\kappa_n = \kappa_0 + n$$\mu_n = \frac{\kappa_0\mu_0 + n \bar{x}}{\kappa_n}$$\alpha_n = \alpha_0 + \frac{n}{2}$$\beta_n = \beta_0 + \frac{1}{2}\sum(x_i - \bar{x})^2 + \frac{\kappa_0n(\bar{x}-\mu_0)^2}{2\kappa_n}$
也就是说,我们的后验分布为:
$$\sigma_\text{post}^2 \sim \text{InvGamma}(\alpha_n, \beta_n)$$
$$\mu_\text{post}|\sigma_\text{post}^2 \sim \mathcal{N}(\mu_n, \frac{\sigma_\text{post}^2}{\kappa_n})$$
这里有两点需要格外注意,第一点,上面给出的公式,如果是逐点更新 (incremental updating) 后验分布参数的话,那么 $n = 1, \bar{x} = x_i$。 如果批量更新 (batch updating),也就是先把所有的数据点都算完,我们知道了每个簇包含的所有点之后再一起更新参数,那 $n$ 是该簇总共有多少个数据点,$\bar{x}$ 是这些数据的均值。通常来说,为了计算方便,我们更倾向使用批量更新。
如果使用批量更新,我们需要最后得到每一个簇的 $n$ 与 $\bar{x}$。那我们在逐点计算的时候,需要更新 $X_k = \{x_i|z_i = k\}$,也就是把每一个数据点 $x_i$ 分配到一个具体的簇。但是根据公式 (1),任一数据点的簇所属是一个分布,即 $P(z_i = k|x_i)$,而非一定值。
我们主要有两种处理方法:
-
最大后验估计 (Maximum A Posteriori, MAP)。也就是找到
$P(z_i = k|x_i)$最大时对应的$k^*$。 -
随机采样。从
$P(z_i = k|x_i)$按照权重随机采样,得到一个具体的$k$。
我们通常选择第二种方法,这样可以保留不确定性。
公式 (1) #
但是在计算公式 (1) 的时候,我们就没有那么幸运了。如果精确计算的话,我们必须用上面的双重积分公式来计算 $P(x_i|\mu_k, \sigma_k^2)$。这种计算很复杂,为了简化,我们最好让 $\mu_k$ 和 $\sigma_k^2$ 是一个具体的值,而不是分布,这样的话,直接带入正态分布的密度函数就好了。那如何找到这两个具体的值?
我们知道 $\mu_k, \sigma_k^2 \sim P(\mu_k, \sigma_k^2|X_k)$,那我们可以
- 随机采样。从该后验分布中,随机采多个值,计算
$P(x_i|\mu_k, \sigma_k^2)$,然后取平均值:
$$P(x_i|\mu_k, \sigma_k^2) = \frac{1}{S} \sum_{s=1}^S P(x_i|\mu_k^{(s)}, \sigma_k^{2(s)}) \tag{5}$$
其中 $S$ 是采样次数。
这里我想多介绍一下。这种方法被称为蒙特卡洛积分 (Monte Carlo integration )。我们上面提到过,公式四的本质就是一个取加权平均的过程。它非常复杂,解析解很难获得。我们的办法是从参数函数中采样,这本身就包含了「加权」,因为高概率区域采样频率高,贡献大,反之亦然。
- 最大后验估计 (Maximum A Posteriori, MAP),也就是取密度最高的值。
一般情况下,我们选择随机采样以保留不确定性。
对于 $P(z_i = k)$,一般的教材中都直接用 Dirichlet Process 或者 Chinese Restaurant Process,但我们为了简单,不假设有无数个簇。而是说:我们知道可能是两个簇,不确定,但肯定不会多于 10 个簇。那我们就用均匀分布 Uniform Distribution。当然也可以可以用多项分布,Multinomial Distribution 等。因为数据如果够多,先验分布没那么重要,我们还是用均匀分布来做简单计算。
总结 #
我们来总结一下计算的流程,也就是具体的算法。
我们是逐点计算:遍历每一个数据点。对于公式 (2),根据共轭先验,我们使用该簇所包含的数据点数量 $n$ 以及这些数据点的均值 $\bar{x}$, 就可以直接更新簇参数后验分布 $P(\mu_k,\sigma_k^2|X_k)$。但是由于给定一个数据点的簇分布 $P(z_i=k|x_i)$ 非具体值,我们选择单次随机采样,得到一个具体的 $k$。这样对于所有的数据点遍历之后,我们就知道了每个簇的 $n$ 与 $\bar{x}$。
公式 (1) 中,$P(x_i|\mu_k, \sigma_k^2)$ 的精确计算需要双重积分这种高强度计算,我们选择避开它,对参数后验分布 $P(\mu_k,\sigma_k^2|X_k)$ 进行多次随机采样,得到多个 $\mu_k$ 和 $\sigma_k^2$,然后将数据点 $x_i$ 带入 $\mathcal{N}(\mu, \sigma^2)$ 的概率密度函数 (PDF) 中,得到多个 $P(x_i|\mu_k, \sigma_k^2)$ 值之后取平均值。这个过程要对每一个簇 ($k$) 进行,这样才能得到我们想要的离散分布 (该数据点属于不同簇的概率分布)。
开工 #
Talk is cheap, show me the code.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.stats import invgamma
import time
from collections import defaultdict
from numba import jit
Show Code
np.random.seed(42)
n_female = 600
mu_female = 162
sd_female = 6
n_male = 1000 - n_female
mu_male = 175
sd_male = 7
female_heights = np.random.normal(mu_female, sd_female, n_female)
male_heights = np.random.normal(mu_male, sd_male, n_male)
heights = np.concatenate([female_heights, male_heights])
np.random.shuffle(heights)
data = heights.copy()
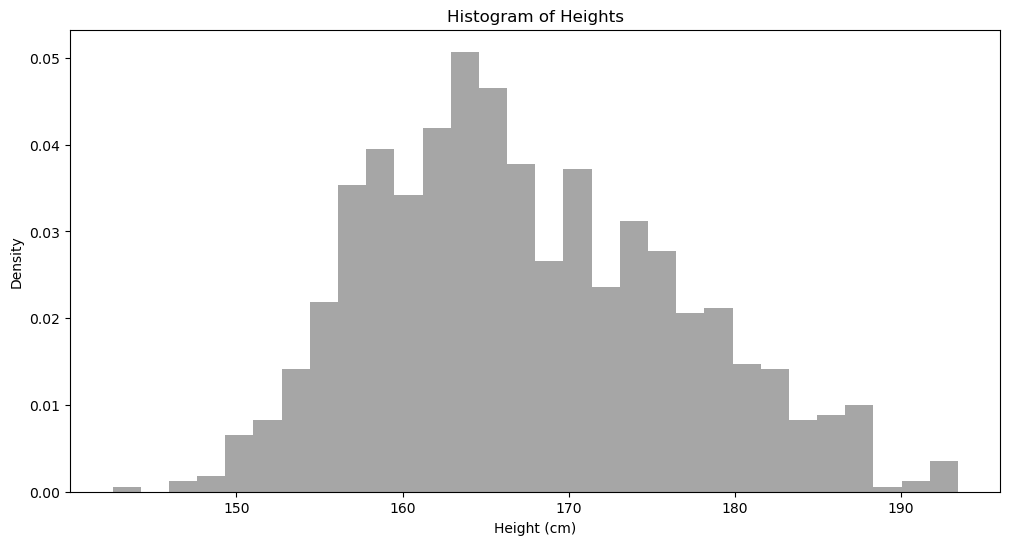
plt.figure(figsize=(12, 6))
plt.hist(data, bins = 30, density=True, alpha=0.7, color='gray')
plt.title('Histogram of Heights')
plt.xlabel("Height (cm)")
plt.ylabel("Density")
plt.show()
# setting
iterations = 10
nclusters = 10
nsampling = 10
# history of P(z_i=k|x_i)
p1_history = []
# history of P(mu_k, sigma_k|X_k)
params_history = []
default_cluster_params = {}
for k in range(nclusters):
default_cluster_params[k] = {
'mu': np.random.uniform(min(data), max(data)),
'kappa': 1,
'alpha': 1,
'beta': np.var(data)
}
cluster_params = default_cluster_params.copy()
start_time = time.time()
# Initialize P(z_i = k) as uniform distribution
P_z = np.ones(nclusters)/nclusters
for it in range(iterations):
# if assignments = [2] means the first data point belongs to the 3rd cluster
assignments = []
# Initialize a list to store p1 for all data points in this iteration
p1_iteration = []
for d in data:
# Step 1: Calculate P(z_i = k | x_i)
# Length is nclusters.
p1 = []
# for each cluster, sample and
# get weighted average of P(x_i|mu_k, sigma_k^2)
for k in range(nclusters):
mus = []
sigmas = []
for _ in range(nsampling):
sigma2 = invgamma.rvs(
cluster_params[k]['alpha'],
scale = cluster_params[k]['beta']
)
sigma = np.sqrt(sigma2)
mu = norm.rvs(
cluster_params[k]["mu"],
sigma/np.sqrt(cluster_params[k]['kappa'])
)
mus.append(mu)
sigmas.append(sigma)
# norm.pdf() result is too small, use LogSumExp to escape underflow
log_likelihoods = [norm.logpdf(
d, mu, sigma) for mu, sigma in zip(mus, sigmas)]
max_log_likelihood = np.max(log_likelihoods)
log_sum_exp = max_log_likelihood + np.log(
np.sum(np.exp(log_likelihoods - max_log_likelihood)))
average_likelihood = np.exp(log_sum_exp)/len(log_likelihoods)
# Multiply by prior P(z_i = k), according to Eq (1) in main text
p1.append(P_z[k] * average_likelihood)
# Step 2: Assign data point to a cluster
if np.sum(p1) == 0:
probs = np.ones(nclusters)/nclusters
else:
probs = p1 / np.sum(p1)
# 0-9
choice = np.random.choice(nclusters, p=probs)
assignments.append(choice)
# Store p1 for the current data point
p1_iteration.append(p1.copy())
# Update P(z_i = k)
P_z = np.zeros(nclusters)
for k in range(nclusters):
P_z[k] = np.sum(np.array(assignments) == k)/len(data)
# Step 3: Batch update cluster parameters of P(mu_k, sigma_k^2|X_k)
for k in range(nclusters):
cluster_data_idx = [i for i, val in enumerate(assignments) if val == k]
cluster_data = data[cluster_data_idx]
n = len(cluster_data)
if n == 0:
# if cluster is empty, no need to calculate below
# move on to the next k
continue
x_bar = np.mean(cluster_data)
k_params = default_cluster_params[k]
kappa_n = k_params['kappa'] + n
mu_n = (k_params['kappa'] * k_params['mu'] + n * x_bar) / kappa_n
alpha_n = k_params['alpha'] + 0.5 * n
beta_n = k_params['beta'] + 0.5 * np.sum((cluster_data - x_bar)**2) + (
k_params['kappa'] * n * (x_bar - k_params['mu'])**2) / (2 * kappa_n)
cluster_params[k] = {
'mu': mu_n,
"kappa": kappa_n,
"alpha": alpha_n,
"beta": beta_n
}
# keep data from this iteration
if (it + 1)%1 == 0:
elapsed = time.time() - start_time
print(f"Iteration {it+1} completed! Time elapsed: {elapsed:.2f}s")
# Make a copy
p1_history.append(list(p1_iteration))
params_history.append([cluster_params[k] for k in range(nclusters)])
每次迭代后,assignments 记录了每个点的簇归属。那我们可以用这个来更新 $P(z_i = k)$。也就是说,虽然我们一开始 $P(z_i = k)$ 用的是均匀分布,但第一次迭代后,以及每次迭代后,就可以根据最新的 assignments 来更新它。
p1_iteration 记录某一具体迭代中所有的 p1,而 p1 是一个具体数据点在所有簇上的未归一化后验概率 (Unnormalized Posterior Probability),也就是公式一中的 $P(z_i = k) \cdot P(x_i|\mu_k, \sigma_k^2)$。而 p1_history 是所有 p1_iteration 的集合。
这里有一个问题,我们需要在把 p1 放进 p1_iteration 之前进行标准化吗?答案是不需要。
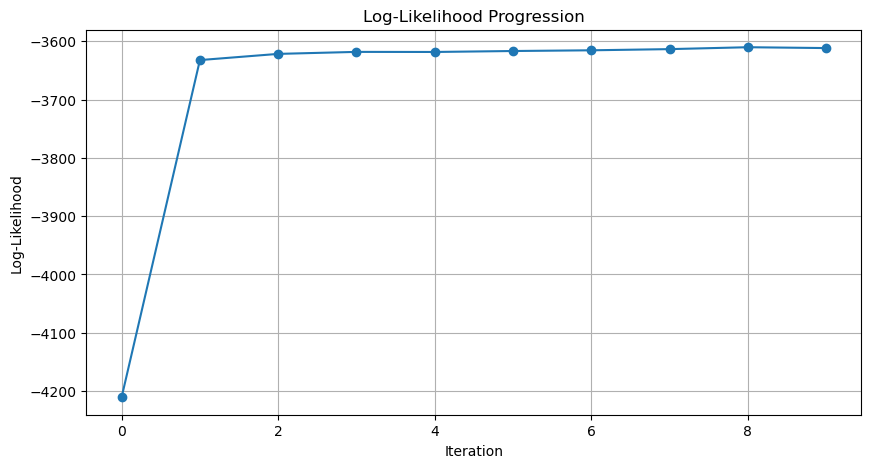
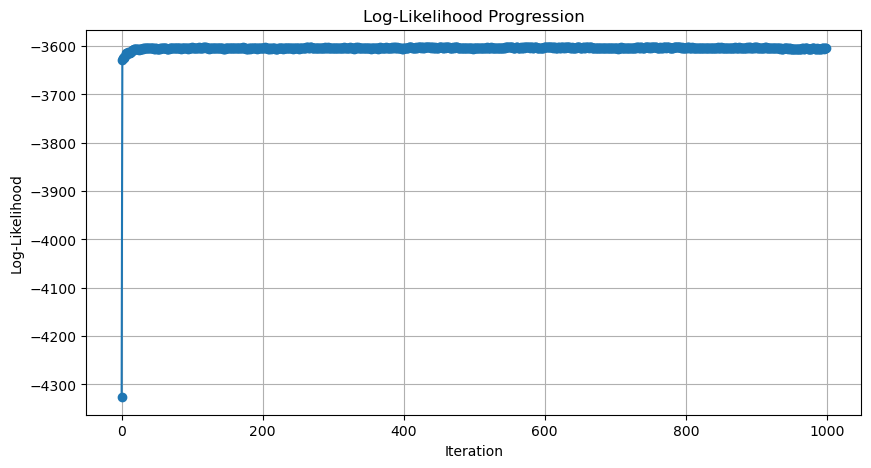
我们记录 p1_history 的目的是什么?最主要的目的是看模型是否收敛。那怎么判断模型是否收敛?通过计算并画出每次迭代后整体数据的可能性,即:
$$P(X) = \prod_{i=1}^{n} P(x_i)$$
其中 $X$ 代表所有的数据点,$n$ 表示数据量。
直接如此计算会导致算术下溢 (Arithmetic underflow) 。我们通常计算对数似然:
$$\log P(X) = \sum_{i=1}^n \log P(x_i)$$
那 $P(x_i)$ 是什么?它是边际似然 (Marginal Likelihood) 或者证据 (Evidence)。它也是公式一中的归一化参数。
细看一下公式一:
$$P(z_i = k|x_i) = \frac{P(x_i|z_i = k) P(z_i = k)}{P(x_i)} = \frac{P(x_i|z_i = k) P(z_i = k)}{\sum_{k'} P(x_i | z_i = k') P(z_i = k')}$$
所以 $P(x_i)$ 就是 sum(p1)。理解了这一点你也就理解了全部。
我们接下来看一下如何计算与每一次迭代相对应的 log likelihood。这样,计算所有迭代的结果后,我们就可以画出似然变化趋势图 (Likelihood Progression)。
def compute_log_likelihood(p1_iteration: np.ndarray) -> float:
"""计算单次迭代的 log-likelihood"""
# p_x = np.sum(p1_iteration, axis=1) # 计算所有数据点的 P(x_i)
# This is to account for when we use dp as prior later
p_x = np.array([np.sum(p1) for p1 in p1_iteration])
return np.sum(np.log(p_x + 1e-10)) # 避免 log(0)
def obtain_log_likelihoods(p1_history: np.ndarray) -> list:
"""计算所有迭代的 log-likelihood"""
return [compute_log_likelihood(p1_iteration) for p1_iteration in p1_history]
Show Code
def extract_cluster_means_and_variances(params, nclusters):
"""
Extract cluster means and variances over iterations from parameter history.
Args:
params (list): A list of cluster parameters for each iteration.
nclusters (int): Number of clusters.
Returns:
cluster_means (dict): Mean values for each cluster across iterations.
cluster_variances (dict): Variance values for each cluster across iterations.
"""
iterations = len(params) # Number of iterations
cluster_means = {k: [] for k in range(nclusters)}
cluster_variances = {k: [] for k in range(nclusters)}
# Extract means and variances for each cluster
for it in range(iterations):
for k in range(nclusters):
cluster_means[k].append(params[it][k]['mu'])
cluster_variances[k].append(1 / params[it][k]['alpha']) # Approximation for variance
return cluster_means, cluster_variances
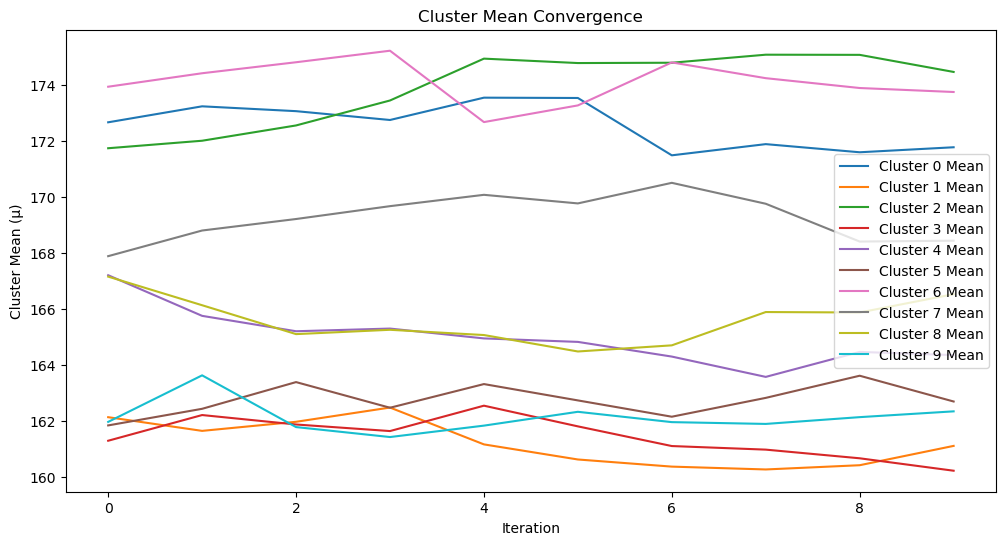
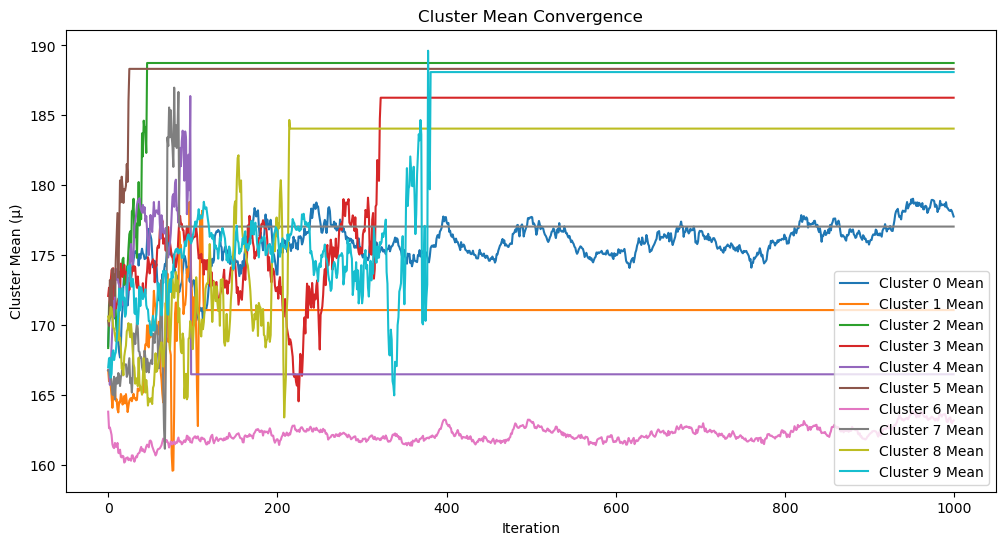
def plot_cluster_means(cluster_means, iterations):
"""
Plot the convergence of cluster means over iterations.
Args:
cluster_means (dict): Mean values for each cluster across iterations.
iterations (int): Total number of iterations.
"""
plt.figure(figsize=(12, 6))
for k, means in cluster_means.items():
plt.plot(range(iterations), means, label=f"Cluster {k} Mean")
plt.xlabel("Iteration")
plt.ylabel("Cluster Mean (μ)")
plt.title("Cluster Mean Convergence")
plt.legend()
plt.show()
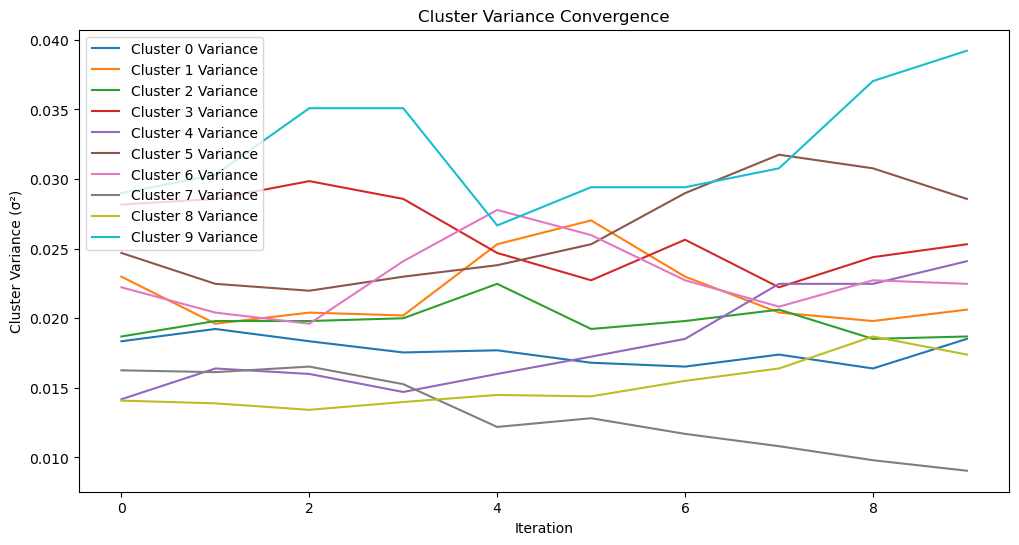
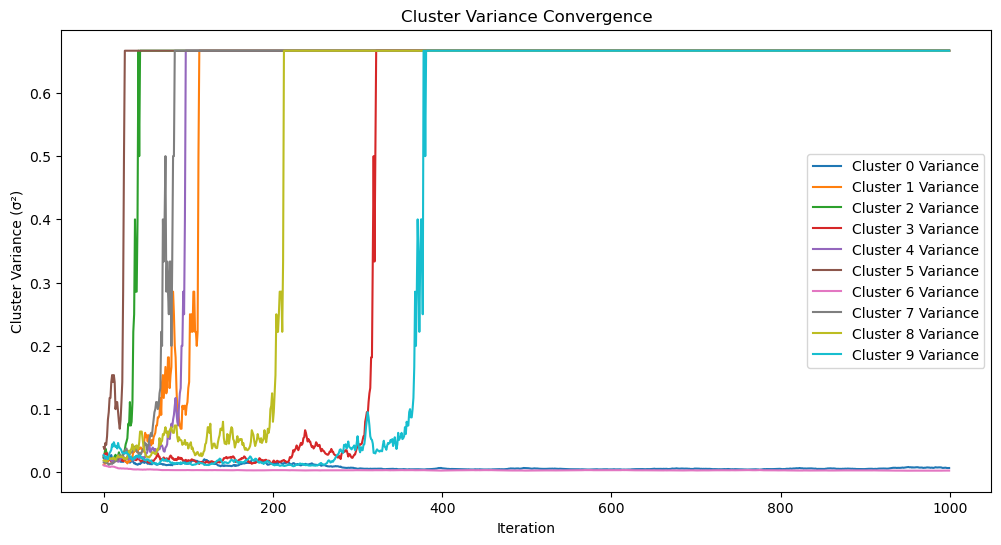
def plot_cluster_variances(cluster_variances, iterations):
"""
Plot the convergence of cluster variances over iterations.
Args:
cluster_variances (dict): Variance values for each cluster across iterations.
iterations (int): Total number of iterations.
"""
plt.figure(figsize=(12, 6))
for k, variances in cluster_variances.items():
plt.plot(range(iterations), variances, label=f"Cluster {k} Variance")
plt.xlabel("Iteration")
plt.ylabel("Cluster Variance (σ²)")
plt.title("Cluster Variance Convergence")
plt.legend()
plt.show()
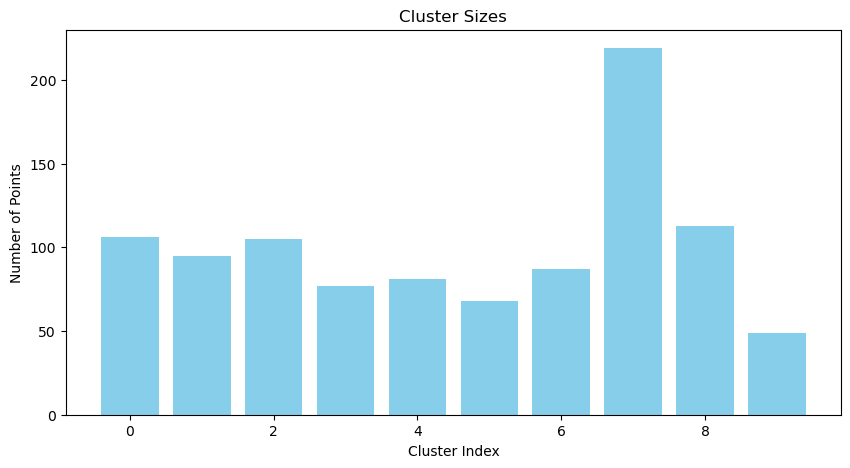
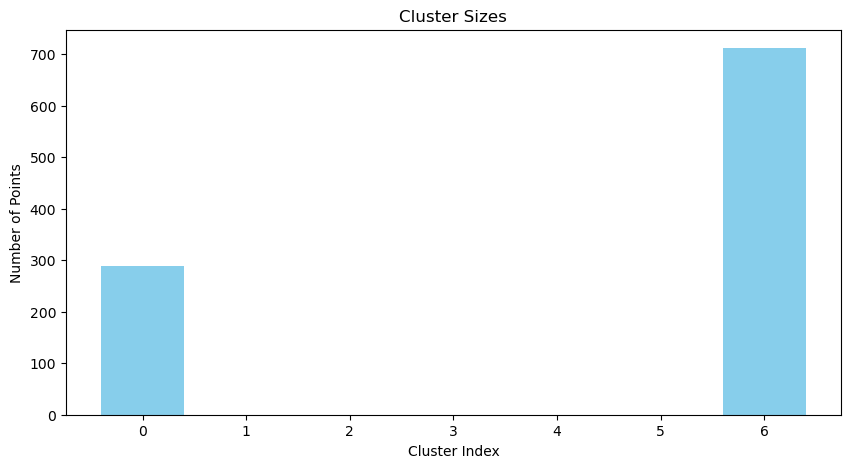
# Step 2: Bar chart for cluster sizes
def plot_cluster_sizes(assignments):
cluster_sizes = np.bincount(assignments)
plt.figure(figsize=(10, 5))
plt.bar(range(len(cluster_sizes)), cluster_sizes, color='skyblue')
plt.title("Cluster Sizes")
plt.xlabel("Cluster Index")
plt.ylabel("Number of Points")
plt.show()
def plot_log_likelihood_progression(p1s):
log_likelihoods = obtain_log_likelihoods(p1s)
# 画图
plt.figure(figsize=(10, 5))
plt.plot(log_likelihoods, marker='o', linestyle='-')
plt.title("Log-Likelihood Progression")
plt.xlabel("Iteration")
plt.ylabel("Log-Likelihood")
plt.grid()
plt.show()
plot_cluster_sizes(assignments)
# Extract cluster means and variances
cluster_means, cluster_variances = extract_cluster_means_and_variances(params_history, nclusters)
# Plot cluster means
plot_cluster_means(cluster_means, len(params_history))
# Plot cluster variances
plot_cluster_variances(cluster_variances, len(params_history))
plot_log_likelihood_progression(p1_history)
优化 #
我们看到,我们的算法非常慢,10 次迭代竟然需要一分钟!下面我尝试通过「向量运算」的方式进行优化:
-
把
[norm.logpdf(d, mu, sigma) for mu, sigma in zip(mus, sigmas)]变成下面的calculate_average_likelihood(d, mus, sigmas)。这样我们就避免了 for loop。 -
我们是逐点计算
$P(\mu_k, \sigma^2_k|X_k)$,这本身没问题,但是我们没必要逐点对每个簇的参数,即$\mu$与$\sigma^2_k$,进行采样。这是因为,采样由每个簇的参数后验决定,而参数后验是在每次迭代结束的时候才更新,而不是逐点更新。所以我们在每次迭代开始时、遍历每个数据点之前对$\mu$与$\sigma^2_k$进行采样和估值即可。
# Dirichlet multinomial
@jit(nopython=True)
def calculate_average_likelihood(d: float, mus: np.ndarray, sigmas: np.ndarray):
"""Vectorized log likelihood calculation with numerical stability.
Args:
d: A scalar or np.array of data points.
mus: A np.ndarray of means.
sigmas: A np.ndarray of standard deviations.
Returns:
The average likelihood.
log(exp(-(x-μ)²/(2σ²)) / sqrt(2πσ²))
= -(x-μ)²/(2σ²) - log(sqrt(2πσ²))
= -(x-μ)²/(2σ²) - 0.5*log(2π) - log(σ)
"""
# Calculate log likelihoods
log_likelihoods = -0.5 * np.log(2 * np.pi) - np.log(sigmas) - \
0.5 * ((d - mus) / sigmas) ** 2
# Use log-sum-exp trick for numerical stability
max_log_likelihood = np.max(log_likelihoods)
log_sum_exp = max_log_likelihood + np.log(
np.sum(np.exp(log_likelihoods - max_log_likelihood)))
# Return the average likelihood
return np.exp(log_sum_exp) / len(mus)
# setting
iterations = 1000
nclusters = 10
nsampling = 10
# history of P(z_i=k|x_i)
p1_history = []
# history of P(mu_k, sigma_k|X_k)
params_history = []
n_data = len(data)
default_cluster_params = {}
for k in range(nclusters):
default_cluster_params[k] = {
'mu': np.random.uniform(min(data), max(data)),
'kappa': 1,
'alpha': 1,
'beta': np.var(data)
}
cluster_params = default_cluster_params.copy()
start_time = time.time()
# Initialize P(z_i = k) as uniform distribution
P_z = np.ones(nclusters) / nclusters
for it in range(iterations):
# For each cluster, sample and get weighted average of P(x_i|mu_k, sigma_k^2)
all_mus = {}
all_sigmas = {}
for k, k_params in cluster_params.items():
sigma2_samples = invgamma.rvs(
k_params['alpha'],
scale = k_params['beta'],
size = nsampling
)
sigma_samples = np.sqrt(sigma2_samples)
mu_samples = norm.rvs(
k_params["mu"],
sigma_samples/np.sqrt(k_params['kappa'])
)
all_mus[k] = mu_samples
all_sigmas[k] = sigma_samples
# Assigning each data point to a cluster
assignments = np.zeros(n_data, dtype = np.int64)
# Store the prob of this data point belonging to different specific clusters
p1 = np.ndarray(shape=(n_data, nclusters), dtype = float)
for idx, d in enumerate(data):
# Step 1: Calculate P(z_i = k | x_i) for all clusters
for k_idx, k in enumerate(cluster_params.keys()):
# Prior times likelihood
p1[idx][k_idx] = P_z[k] * calculate_average_likelihood(d, all_mus[k], all_sigmas[k])
# Step 2: Assign data point to a cluster
if np.sum(p1[idx]) == 0:
probs = np.ones(nclusters)/nclusters
else:
probs = p1[idx] / np.sum(p1[idx])
# 0-9
choice = np.random.choice(nclusters, p=probs)
assignments[idx] = choice
# Step 3: Update P(z_i = k)
# minlenth = nclusters here makes sure all clusters have a prob
# Just imagine assignments is all 1s: [1, 1, 1, 1, 1]
P_z = np.bincount(assignments, minlength=nclusters) / n_data
# Step 4: Batch update cluster parameters of P(mu_k, sigma_k^2|X_k)
for k in range(nclusters):
cluster_data_idx = [i for i, val in enumerate(assignments) if val == k]
cluster_data = data[cluster_data_idx]
n = len(cluster_data)
if n == 0:
# if cluster is empty, no need to calculate below
# move on to the next k
continue
x_bar = np.mean(cluster_data)
k_params = default_cluster_params[k]
kappa_n = k_params['kappa'] + n
mu_n = (k_params['kappa'] * k_params['mu'] + n * x_bar) / kappa_n
alpha_n = k_params['alpha'] + 0.5 * n
beta_n = k_params['beta'] + 0.5 * np.sum((cluster_data - x_bar)**2) + (
k_params['kappa'] * n * (x_bar - k_params['mu'])**2) / (2 * kappa_n)
cluster_params[k] = {
'mu': mu_n,
"kappa": kappa_n,
"alpha": alpha_n,
"beta": beta_n
}
# keep data from this iteration
if (it + 1)%100 == 0:
elapsed = time.time() - start_time
print(f"Iteration {it+1} completed! Time elapsed: {elapsed:.2f}s")
p1_history.append(p1.copy())
params_history.append([cluster_params[k] for k in cluster_params.keys()])
plot_cluster_sizes(assignments)
# Extract cluster means and variances
cluster_means, cluster_variances = extract_cluster_means_and_variances(
params_history, nclusters)
# Plot cluster means
plot_cluster_means(cluster_means, len(params_history))
# Plot cluster variances
plot_cluster_variances(cluster_variances, len(params_history))
plot_log_likelihood_progression(p1_history)
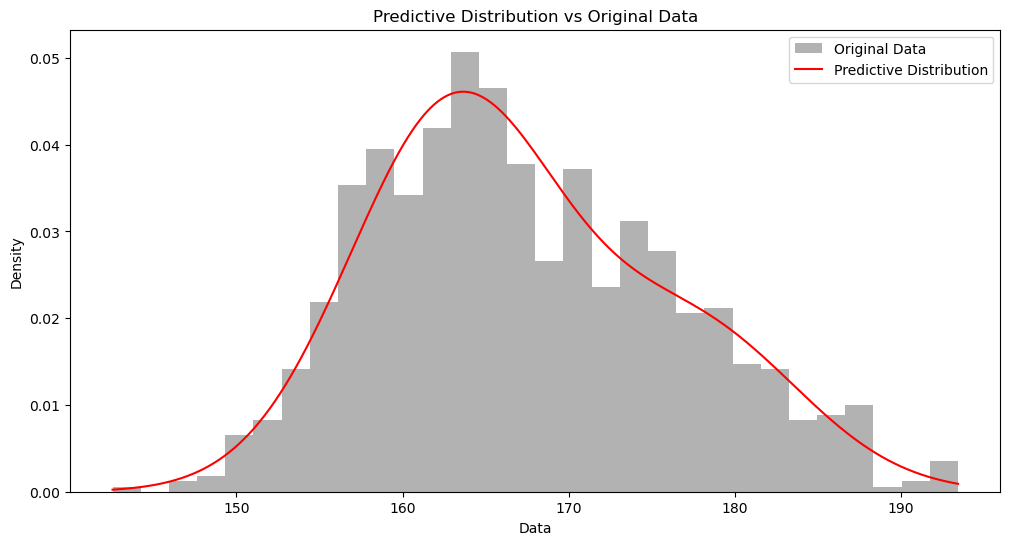
后验预测分布 #
我们可以用后验预测分布 (Posterior Predictive Distribution) 来检测我们的模型是否正确。
上面,我们的代码最后有两个结果:assignments 和 cluster_params。前者是每个数据点的簇所属,后者是每个簇的后验分布参数。
那如果我问你,两个新的数据点,$166$ 和 $176$,哪个出现的概率比较大?为了回答这个问题,比较「一劳永逸」的方法是从负无穷到正无穷这个区间,我们计算出每个数据点的概率密度 (Probability Density)。这就是后验预测分布。
从数学上来看,我们是在计算
$$P(X_\text{new}) = \sum_{k=1}^K P(z_\text{new}=k)\cdot P(X_\text{new}|\mu_k, \sigma_k)$$
其中 $X_\text{new}$ 表示的是从负无穷到正无穷这个区间上的连续值,而非一个具体数值。
我们来证明该分布的积分为 1:
$$ \begin{aligned} \int_{-\infty}^{\infty} P(X_\text{new}) dX_\text{new} & = \int_{-\infty}^{\infty} \sum_{k=1}^K P(z_\text{new}=k)\cdot P(X_\text{new}|\mu_k, \sigma_k) dX_\text{new}\\ & = \sum_{k=1}^K P(z_\text{new}=k) \int_{-\infty}^{\infty} P(X_\text{new}|\mu_k, \sigma_k) dX_\text{new} \\ & = 1 \cdot 1 \\ & = 1 \end{aligned} $$
在真实计算时,有两个问题需要考量。第一,我们不需要算 $(-\infty, \infty)$ 这个区间所有的 $X_\text{new}$。为了检验模型的准确性,我们只需要计算原本数据的区间就可以,即 $X_{\text{new}} \in [\min(\text{data}), \max(\text{data})]$。
其次,$P(X_\text{new}|\mu_k, \sigma_k)$ 无法直接结算,因为 $\mu_k, \sigma_k$ 是分布,而非具体值。我们采用随机采样,然后取平均值。我们在公式 (4) 提到过。
from typing import Dict
def posterior_predictive(
x_new:np.ndarray,
assignments: np.ndarray,
cluster_params:Dict[int, Dict[str, float]],
nsampling: int = 100
) -> np.ndarray:
"""
Obtain posterior predictive likelihoods for every float in x_new
"""
px_new = np.zeros_like(x_new, dtype=np.float64)
# P_z: P(z_i = k)
P_z = np.bincount(assignments, minlength=len(cluster_params)) / len(assignments)
# Iterate through all clusters
# We should resample rather than using all_mus and all_sigmas because those are not baesd on the
# second last iteration cluster_prams, not the result of the last iteration
for k, k_params in cluster_params.items():
# Sampling sigma and mu
sigma2_samples = invgamma.rvs(
k_params['alpha'],
scale = k_params['beta'],
size = nsampling
)
sigma_samples = np.sqrt(sigma2_samples)
mu_samples = norm.rvs(
k_params["mu"],
sigma_samples/np.sqrt(k_params['kappa'])
)
avg_likelihood = np.array([
calculate_average_likelihood(x, mu_samples, sigma_samples)
for x in x_new
])
px_new += P_z[k] * avg_likelihood
return px_new
def plot_predictive_distribution(
data,
assignments,
cluster_params,
bins=30,
nsampling=100
):
# Generate predictive distribution
x_vals = np.linspace(min(data), max(data), 1000)
predictive_pdf = posterior_predictive(x_vals, assignments, cluster_params, nsampling)
# Plot results
plt.figure(figsize=(12, 6))
# Plot histogram of data
plt.hist(data, bins=bins, density=True, alpha=0.6, color='gray', label='Original Data')
# Plot predictive distribution
plt.plot(x_vals, predictive_pdf, label='Predictive Distribution', color='red')
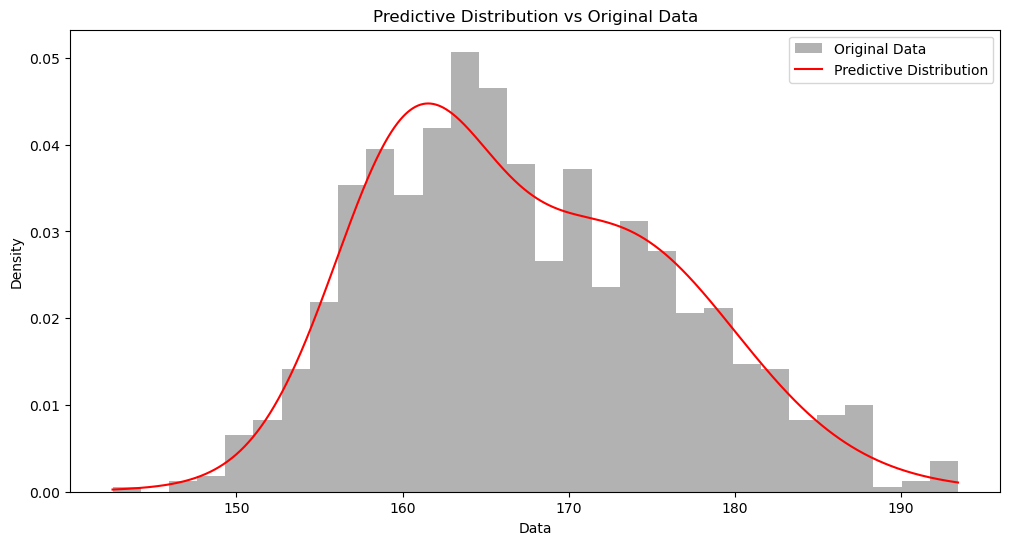
plt.title('Predictive Distribution vs Original Data')
plt.xlabel('Data')
plt.ylabel('Density')
plt.legend()
plt.show()
plot_predictive_distribution(data, assignments, cluster_params)
用 Dirichlet Process 当作先验 #
我们上面用的是均匀分布做先验,这需要我们提前假设一个可能的簇数。但如果我们不想假设怎么办?
可以选择用 Dirichlet Process 做先验分布。这样,我们不用提前设定有多少个簇,而是通过设定 alpha 来决定新开一个簇的概率。
根据 Dirichlet Process 或者中餐馆过程 ,一个新的数据点属于某个大簇的概率要大于无限个很小的簇,这符合贝叶斯统计后验概率的更新逻辑。
完整代码如下:
# Initialization
dp_alpha = 2
iterations = 1000
nsampling = 100
ndata = len(data)
# Default Parameters
default_params = {
'mu': np.mean(data),
'kappa': 1, # Lower = more spread in means
'alpha': 1, # Lower = more variance in cluster widths
'beta': np.var(data) # Higher = wider clusters
}
# Record parameters
cluster_params = {0:default_params.copy()}
p1_history = []
params_history = []
assignments = np.zeros(ndata, dtype=np.int64)
assignments_history = []
start_time = time.time()
for it in range(iterations):
# Initialize a list to store p1 for all data points in this iteration
p1_iteration = np.empty(ndata, dtype=object)
# Sample mus and sigmas for each cluster
all_mus = {}
all_sigmas = {}
for k, k_params in cluster_params.items():
sigma2_samples = invgamma.rvs(k_params['alpha'], scale = k_params['beta'], size = nsampling)
sigma_samples = np.sqrt(sigma2_samples)
mu_samples = norm.rvs(k_params["mu"], sigma_samples/np.sqrt(k_params['kappa']))
all_mus[k] = mu_samples
all_sigmas[k] = sigma_samples
for idx, d in enumerate(data):
# Step 1: Assign each data point to a cluster
# For the first data point, assign it to the first table
if idx == 0:
assignments[idx] = 0
p1_iteration[idx] = [calculate_average_likelihood(d, all_mus[0], all_sigmas[0])]
continue
# All existing assignments up until the current data point
curr_assignments = assignments[:idx] # excluding assignments[idx:]
choices = np.arange(0, max(curr_assignments) + 2)
# How many customers are there on kth table
# bincount will consider all nums [0, max(X)]. If a num does not exist, it will be 0
# So bincount will return an array of length of max(X)
n_k = np.bincount(curr_assignments)
# Total "customers" before this data point
curr_total = idx + dp_alpha
probs = np.append(n_k/curr_total, dp_alpha/curr_total)
# This is to calculate p1 below
# key is cluster id, value is the associated probability of assigning this datum to that cluster
curr_prior = dict(zip(choices, probs))
# Step 2: Calculate P(z_i = k | x_i) for all clusters
p1 = np.zeros(len(curr_prior), dtype=float)
for k_idx, k in enumerate(curr_prior.keys()):
# if cluster is new, initiate params for this cluster
if k not in cluster_params:
cluster_params[k] = default_params.copy()
sigma2_samples = invgamma.rvs(default_params['alpha'], scale = default_params['beta'], size = nsampling)
sigma_samples = np.sqrt(sigma2_samples)
mu_samples = norm.rvs(default_params["mu"], sigma_samples/np.sqrt(default_params['kappa']))
all_mus[k] = mu_samples
all_sigmas[k] = sigma_samples
# Prior times the likelihood
p1[k_idx] = curr_prior[k] * calculate_average_likelihood(d, all_mus[k], all_sigmas[k])
p1_iteration[idx] = p1
# Sampling based on posterior
p1_normalized = p1 / np.sum(p1) # Normalization
assignments[idx] = np.random.choice(choices, p=p1_normalized)
# Remove empty clusters from cluster_params
empty_clusters = [x for x in cluster_params.keys() if x not in np.unique(assignments)]
for k in empty_clusters:
del cluster_params[k]
del all_mus[k]
del all_sigmas[k]
# Step 3: Batch update cluster parameters of P(mu_k, sigma_k^2|X_k)
for k in cluster_params.keys():
cluster_data = data[assignments == k]
n = len(cluster_data)
if n == 0:
continue
x_bar = np.mean(cluster_data)
kappa_n = default_params['kappa'] + n
mu_n = (default_params['kappa'] * default_params['mu'] + n * x_bar) / kappa_n
alpha_n = default_params['alpha'] + 0.5 * n
beta_n = default_params['beta'] + 0.5 * np.sum((cluster_data - x_bar)**2) + (
default_params['kappa'] * n * (x_bar - default_params['mu'])**2) / (2 * kappa_n)
cluster_params[k] = {
'mu': mu_n,
"kappa": kappa_n,
"alpha": alpha_n,
"beta": beta_n
}
# keep data from this iteration
if (it + 1) % 100 == 0:
elapsed = time.time() - start_time
print(f"Iteration {it+1} completed! Time elapsed: {elapsed:.2f}s")
p1_history.append(p1_iteration.copy())
params_history.append({k: v.copy() for k, v in cluster_params.items()})
assignments_history.append(assignments.copy())
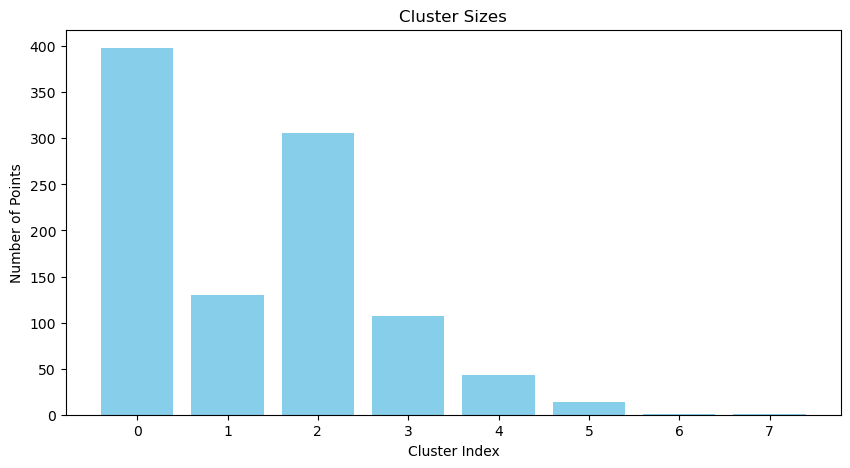
plot_cluster_sizes(assignments)
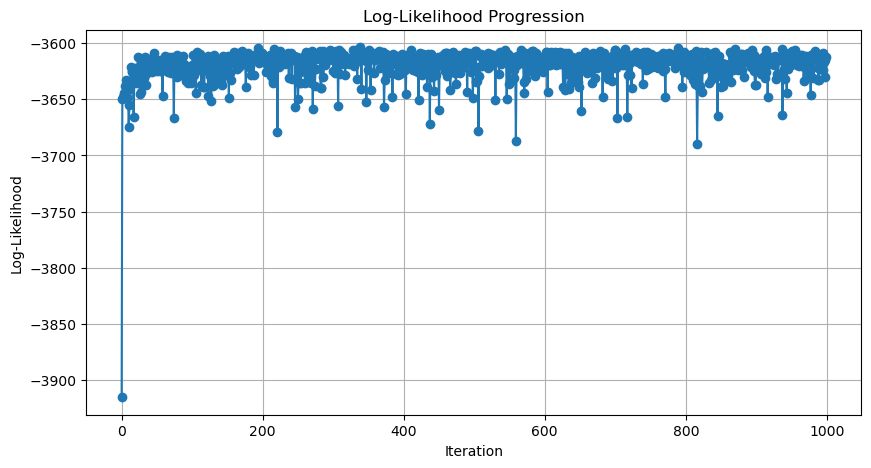
plot_log_likelihood_progression(p1_history)
plot_predictive_distribution(data, assignments, cluster_params)
最后一次修改于 2025-06-03 • 编辑本页