夫一銅錢,有正、反兩面者,其正面為上之概率,若曰 ,則拋之 次,正面朝上者 。其法曰:
是所謂雙項分布者也,西人謂之 Binomial Distribution,吾曾言其法 。
今則反其道推之,既知拋 次而正面朝上者 ,問此銅錢拋一次正面朝上之概率 為何?
倘求一數, 可取 ,然未為必然也。且若余欲得一機率分布,非一定值,則當用貝葉斯之法 ,曰:
吾於銅錢初無所知,故先驗機率 視為均勻分布,西人曰 Uniform Distribution。謂之恒常,取 1 可也。似然機率 ,乃雙項分布是矣,曰:
夫 與 均為恒常,棄之,可得:
此即 Beta 分布之式。若令
此設之,為使 或 時,分布仍得定義,且有意義耳。
則機率分布式可化作:
然欲其為真正之分布,需使其於 區間上積分歸一,曰:
為此,須引歸一常數 ,令:
夫 者:
歐拉 者,西人數學巨擘,其得精妙之法,曰:
乃 Gamma 函數 ,為階乘之推廣。
綜上,Beta 分布之全貌得焉:
或作:
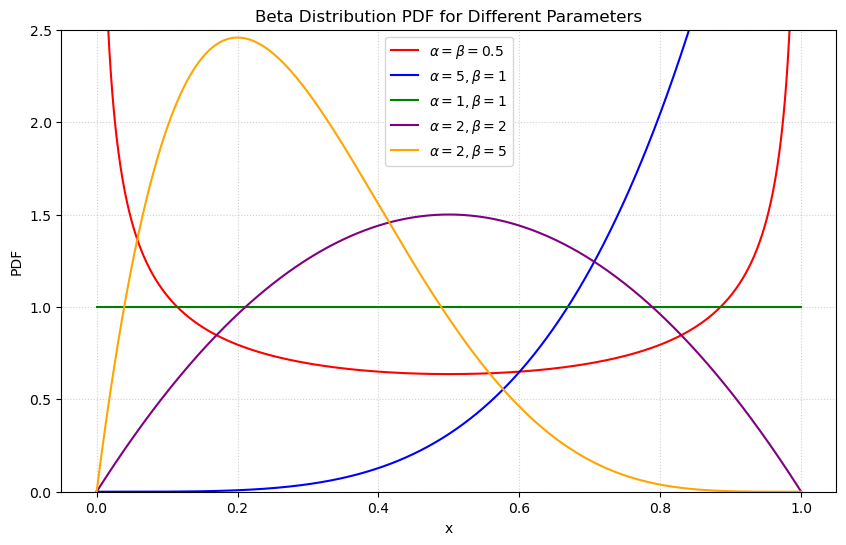
畫之:
Show Code
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# Create the x values
x = np.linspace(0, 1, 1000)
# Create different beta distributions
params = [
(0.5, 0.5, 'red', r'$\alpha = \beta = 0.5$'),
(5, 1, 'blue', r'$\alpha = 5, \beta = 1$'),
(1, 1, 'green', r'$\alpha = 1, \beta = 1$'),
(2, 2, 'purple', r'$\alpha = 2, \beta = 2$'),
(2, 5, 'orange', r'$\alpha = 2, \beta = 5$')
]
# Create the plot
plt.figure(figsize=(10, 6))
# Plot each distribution
for alpha, beta_param, color, label in params:
plt.plot(x, beta.pdf(x, alpha, beta_param), color=color, label=label)
# Customize the plot
plt.grid(True, linestyle=':', alpha=0.6)
plt.xlabel('x')
plt.ylabel('PDF')
plt.ylim(0, 2.5)
plt.legend()
plt.title('Beta Distribution PDF for Different Parameters')
# Show the plot
plt.show()
最后一次修改于 2025-07-02 • 编辑本页