科学研究证明，火星人智商的方差是
$36$，我们不知道其平均值 ($\mu$)。为了知道$\mu$，科学家随机抽取了$16$名火星人，测量他们的智商。科学家的假设是$H_0: \mu = 100$，$H_A: \mu \ne 100$。
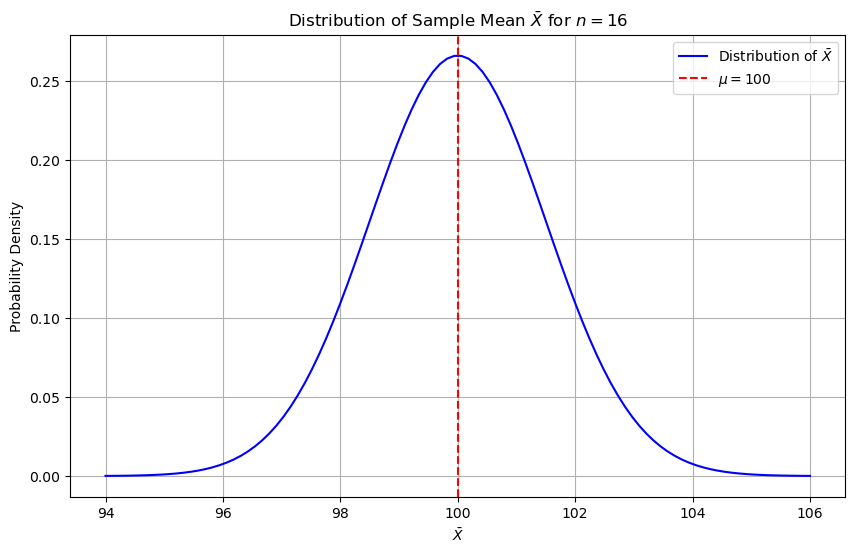
如果把这 16 名火星人的平均智商记为 $\bar{X}$，那根据中心极限定理的知识，我们知道其分布为：
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
mu0 = 100
sigma = np.sqrt(36)
n = 16
# standard error
se = sigma/np.sqrt(n)
xs = np.linspace(mu0 - 4*se, mu0 + 4*se, 100)
y = stats.norm.pdf(xs, mu0, se)
Show Code
plt.figure(figsize=(10,6))
plt.plot(
xs, y,
label=r'Distribution of $\bar{X}$', color='blue')
plt.title(r'Distribution of Sample Mean $\bar{X}$ for $n = 16$')
plt.xlabel(r'$\bar{X}$')
plt.ylabel('Probability Density')
plt.axvline(
mu0, color='red',
linestyle='--', label=r'$\mu = 100$')
plt.legend()
plt.grid(True)
plt.show()
显著水平、一类错误 #
如果 $\alpha = 0.05$，那么 $\bar{X}$ 为多少时，我们会拒绝 $H_0$？
alpha = 0.05
# norm.ppf() 相当于 R 中的 qnorm()
# ppf: percent point function; inverse of cdf
lower_bound = stats.norm.ppf(alpha/2, loc=mu0, scale = se)
upper_bound = stats.norm.ppf(1-alpha/2, loc = mu0, scale = se)
lower_bound, upper_bound
(97.06005402318992, 102.93994597681008)
Show Code
plt.figure(figsize=(10, 6))
plt.plot(xs, y, label=r'Distribution of $\bar{X}$', color='blue')
plt.fill_between(xs, y, where=(xs <= lower_bound), color='orange',
alpha=0.3, label='Rejection Region (Lower)')
plt.fill_between(xs, y, where=(xs >= upper_bound), color='orange',
alpha=0.3, label='Rejection Region (Upper)')
plt.axvline(lower_bound, color='orange', linestyle='--',
label=f'Lower Critical Value ≈ {lower_bound:.2f}')
plt.axvline(upper_bound, color='orange', linestyle='--',
label=f'Upper Critical Value ≈ {upper_bound:.2f}')
plt.axvline(mu0, color='red', linestyle='--', label=r'$\mu = 100$')
plt.title(r'Distribution of Sample Mean $\bar{X}$ with Rejection Regions')
plt.xlabel(r'$\bar{X}$')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()
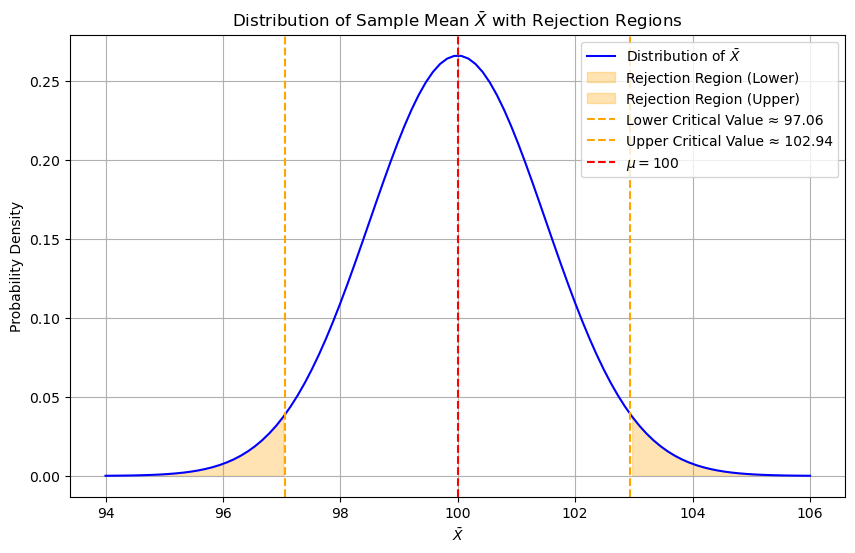上图中的黄色区域被称为「拒绝域」(Rejection Region)。
$\alpha$ 被称为显著水平，或者叫做「一类错误」(Type one error)。它所表达的意思是，本来 $H_0$ 是真相，但我们抽到的数据 (黄色区域中的 $\bar{X}$ 值) 显示 $H_0$ 为真的话不太可能出现这样的 $\bar{X}$，所以我们（错误地）拒绝。
统计功效和二类错误 #
我们来看另外一种情况：$H_0$ 不成立，$H_A：\mu_{A} = 105$ 为真。
$H_A$ 如果成立，$\bar{X}$ 的分布是：
mua = 105
xs = np.linspace(mua - 4*se, mua + 4*se, 100)
y = stats.norm.pdf(xs, mua, se)
Show Code
plt.figure(figsize=(10,6))
plt.plot(
xs, y,
label=r'Distribution of $\bar{X}$', color='blue')
plt.title(r'Distribution of Sample Mean $\bar{X}$ for $n = 16$, Given $H_A$ Being True')
plt.xlabel(r'$\bar{X}$')
plt.ylabel('Probability Density')
plt.axvline(
mua, color='red',
linestyle='--', label=r'$\mu = 100$')
plt.legend()
plt.grid(True)
plt.show()
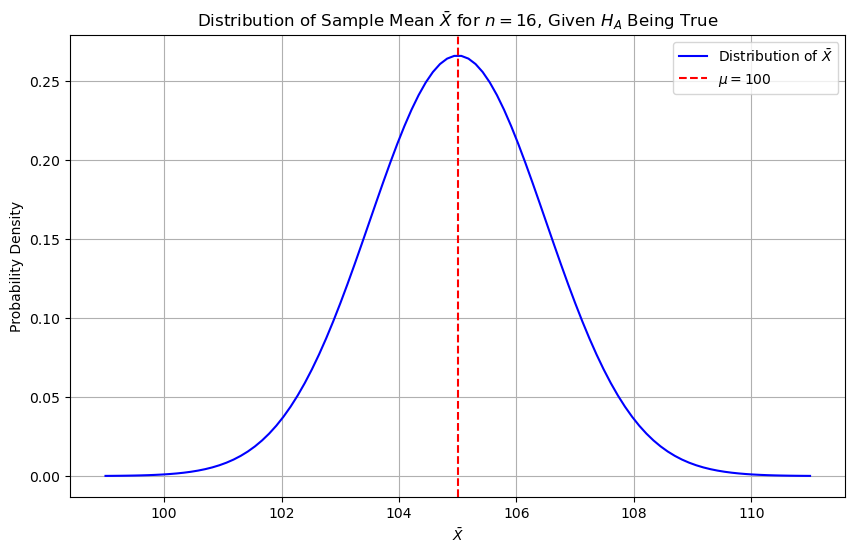那当 $H_A$ 成立时，$\bar{X}$ 落在上图黄色区域，也就是拒绝域，的概率是多大？
lower_region_area = stats.norm.cdf(lower_bound, loc=mua, scale = se)
upper_region_area = 1-stats.norm.cdf(upper_bound, loc=mua, scale = se)
lower_region_area + upper_region_area
0.9151812833018267
我们看到概率大概是 $91.5\%$，这被称为「统计功效」(Power)，也就是说当 $H_0$ 为假、$H_A$ 为真时，我们拒绝 $H_0$ 的概率。
那当 $H_0$ 为假、$H_A$ 为真时，我们也可能会接受 $H_0$，这种情况下我们犯了「二类错误」(Type Two Error)。很明显，Type Two Error = 1 - Power。因为 $H_0$ 为假、$H_A$ 为真时，我们要么接受 $H_0$，要么拒绝，不可能有第三种情况。
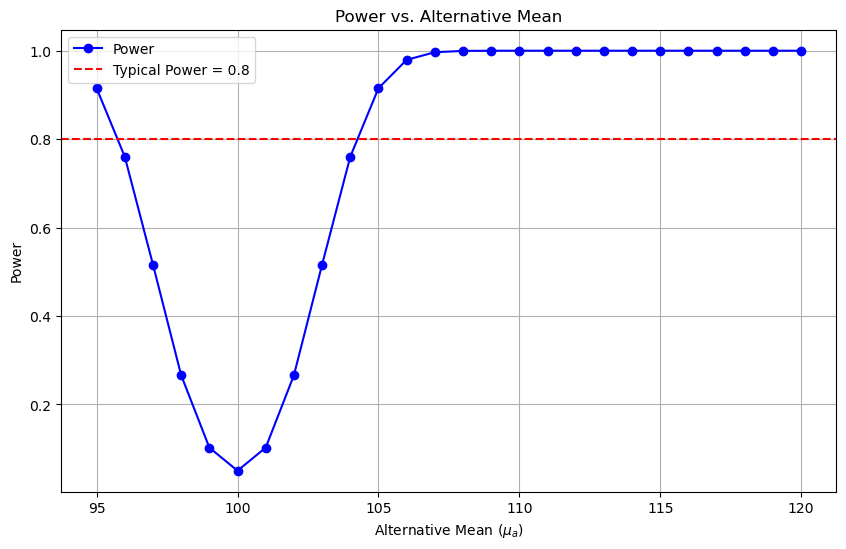
统计功效曲线 #
我们上面算了 $\mu_A = 105$ 的情况，但还可能有别的情况，我们可以都算出来，然后画出所有对应的统计功效。
首先，我们要计算统计功效：
def calc_power(mu0, mua, sigma2, n, alpha):
"""
Inputs:
- mu0: mu when h0 is true
- mua: mu when ha is true
- sigma2: population variance
- n: sample size
- alpha: significance level; type one error
Output:
- power: a float (prob of rejecting H0 when HA is true)
"""
# population sd
sigma = np.sqrt(sigma2)
# standard error; sd for sampling distribution
se = sigma/np.sqrt(n)
# rejection region based on H0
lower_bound = stats.norm.ppf(alpha/2, loc=mu0, scale = se)
upper_bound = stats.norm.ppf(1-alpha/2, loc = mu0, scale = se)
# calculate power under HA
lower_region_area = stats.norm.cdf(lower_bound, loc=mua, scale = se)
upper_region_area = 1-stats.norm.cdf(upper_bound, loc=mua, scale = se)
power = lower_region_area + upper_region_area
return power
calc_power(mu0 = 100, mua = 105, sigma2 = 36, n = 16, alpha = 0.05)
0.9151812833018267
我们把 95 到 120 都算一遍：
start = 95
end = 120
mua_array = np.arange(start, end + 1, 1)
powers = [
calc_power(
mu0 = 100,
mua = x,
sigma2 = 36,
n = 16,
alpha = 0.05
) for x in mua_array
]
Show Code
plt.figure(figsize=(10, 6))
# Use a line plot for smoother visualization
plt.plot(mua_array, powers, marker='o', linestyle='-', color='b', label='Power')
# Add labels and title
plt.xlabel(r'Alternative Mean ($\mu_a$)')
plt.ylabel('Power')
plt.title('Power vs. Alternative Mean')
# Add a horizontal line to indicate a typical power threshold (e.g., 0.8)
plt.axhline(0.8, color='red', linestyle='--', label='Typical Power = 0.8')
# Add a legend and grid
plt.legend()
plt.grid(True)
plt.show()
交互图表 #
如何求 n #
一个思考题是，如果我们知道
- power (1 -
$\beta$)：统计功效 $\sigma^2$: 总体方差$\alpha$: 显著水平$\mu_0$$\mu_A$
如何求 $n$？
其实，方法就藏在 cal_power() 里。
我们知道：
$$P(\bar{X} \le \text{lower bound} | \mu = \mu_A) + P(\bar{X} \ge \text{upper bound} | \mu = \mu_A) = 1 - \beta$$
其中
$$\text{lower bound} = \mu_0 - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}$$
$$\text{upper bound} = \mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}}$$
故而
$$P(\bar{X} \le\mu_0 - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} | \mu = \mu_A) + P(\bar{X} \ge \mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} | \mu = \mu_A) = 1 - \beta$$
我们把
$$P(\bar{X} \le \mu_0 - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} | \mu = \mu_A)$$
转化成 $Z$ 分数：
$$P\left(\frac{\bar{X} - \mu_A}{\sigma / \sqrt{n}} \le \frac{\mu_0 - z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} - \mu_A}{\sigma/\sqrt{n}}\right) = P\left(Z \le \frac{\bar{X} - \mu_A}{\sigma / \sqrt{n}} - z_{\alpha/2}\right)$$
同样
$$P(\bar{X} \ge \mu_0 + z_{\alpha/2} \cdot \frac{\sigma}{\sqrt{n}} | \mu = \mu_A) = P\left(Z \ge \frac{\bar{X} - \mu_A}{\sigma / \sqrt{n}} + z_{\alpha/2}\right)$$
最后的结果是
$$ P\left(Z \le \frac{\bar{X} - \mu_A}{\sigma / \sqrt{n}} - z_{\alpha/2}\right) + P\left(Z \ge \frac{\bar{X} - \mu_A}{\sigma / \sqrt{n}} + z_{\alpha/2}\right)= 1 - \beta$$
我尝试去证明：
$$n = \frac{(z_{\alpha/2} + z_\beta)^2 \cdot \sigma^2}{(\mu_0 - \mu_A)^2}$$
但是我做不到。我还是不知道这个公式是怎么来的。
#统计最后一次修改于 2024-11-15