统计的一个核心问题是,我们想要知道母体 (population) 的情况,但是现实中,母体的情况是未知的,这时我们就需要通过随机抽样的方法,获取样本,通过样本来了解总体。
序章
我们现在来假设一下。
你在北京(A市)上学,有个女朋友,大四快毕业的时候,你考上了新疆((B省)的选调生,不过还好只是呆两年,两年后可以再回A市工作。女朋友拿到了一家互联网公司的offer。那么,一个世纪难题是,离这么远,要不要分手。你们相互谈心,互相觉得,两年的时间还好,也不长,而且通信这么发达,都可以每天微信视频聊天,即使异地恋应该也没问题。于是你们俩决定不分手,坚持异地恋。
好,然后你给你女朋友提出了一个要求。你说你在新疆工作很忙,微信联系的话你觉得不太方便,而且你很传统,喜欢手写的信,你就对你女朋友说:“我走后,你要每周给我写一封情书”。女朋友答应了。
喜获 A 市市长职位,惊闻女友似已变心
你们按原计划进行。你每周都能如约收到一封情书,你很开心。
很快,两年就要过去了,领导看你很棒,把你推荐给了B省的领导,领导知道你想回北京,就把你推荐给了A市的市领导,最终决定让你回去做副市长。
家人觉得你这马上要走上人生巅峰了,可是婚姻大事还没解决,就让你赶紧成婚。你也思考,是啊,和女朋友这么多年了,也该考虑婚姻大事了。你每周都能收到一封信,只是让你不爽的是,你感觉女朋友的情书一次比一次短,最后一封只有四个字:我挺好的。
这几天正好一个朋友来看你,给你八卦说经常看到你女朋友和她同事一起跑步,去健身房。你怀疑你被绿了。
你可马上是副市长的人了,你考虑终身大事的时候可是得慎重些。
你看着手里的情书,蓝瘦,香菇,但又不想轻易相信女朋友已经变心。你突然想到前几天在 Nature 上看到的一篇文章。文章作者声称,他发现人类过去、现在和未来,两个人之间的情书字数符合正态分布,标准差是250 (\(\sigma\)=250)。他还发现,这两个人如果相爱的话,虽然每次情书字数有差别,但平均的话应该是 1500 字。多了少了都不行。这个作者还因为这个发现,获得了诺贝尔“爱情学奖”。
检验
因此,你现在确定的是,女朋友这两年间写的 104 封信的字数是符合正态分布的,标准差是 250。那么,你直接算出来这 104 封信每封信的平均字数,如果平均数正好等于 1500 字的话,说明女朋友还是爱你的。然而,很不凑巧的是,有几天 B 省太冷了,你晚上为了取暖就把几封信(随机地)扔到火堆里取暖(女朋友知道了直接就开除你了),还剩下 25 封情书。所以现在你没办法通过计算总体(104 封情书)的平均字数来断定你女朋友是不是还爱着你了。
你数了数,这25封信的字数分别为:
773 1227 1188 790 1413 1146 1202 776 1400 1240 937 902 1421
1291 1569 1368 939 1363 1331 1088 889 772 683 1374 1535这里说一下,其实这才常见的。大多数情况下我们都不可能获得总体的全部,只能通过抽样来推断总体。
这时候,你突然想到了你了大二的时候学过统计(虽然学得啥都已经送给老师了)。
你开始琢磨了:
你知道你女朋友如果还爱你的话,这 104 封信应该符合 X \(\sim\) N (1500, 250),也就是下面这个分布:
Mean <- 1500
Sd <- 250
# X grid for non-standard normal distribution
x <- seq(-3, 3, length = 100) * Sd + Mean
# Density function
f <- dnorm(x, Mean, Sd)
plot(x, f, type = "l", lwd = 2, col = "blue", ylab = "", xlab = "Weight")
abline(v = Mean) # Vertical line on the mean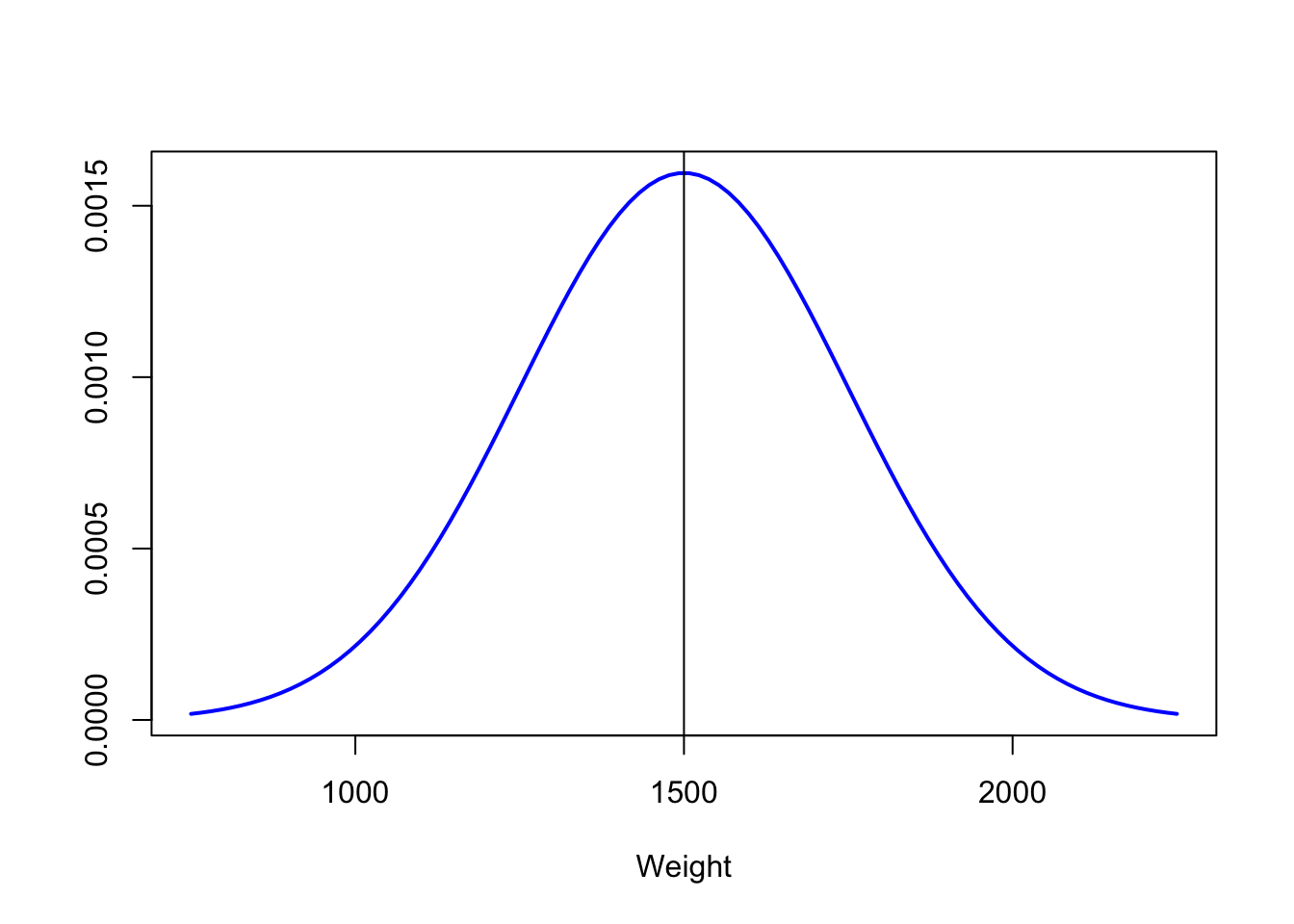
最后一次修改于 2025-06-03 • 编辑本页