Rolling a die #
Imagine you have a 4-sided fair die, with numbers of ‘1’, ‘2’, ‘3’, and ‘4’. You roll the die once and ask your friend, who have his eyes closed, to figure out the outcome. Your friend can ask you any questions, for example, ‘Is the outcome 1?’ or ‘Is it below 3?’. However, you can only respond with ‘Yes’ or ‘No’.
Here is the challenge: which strategy can guarantee that, on average, your friend asks the least number of questions to figure out the outcome?
Let’s take one strategy as an example: Asking ‘Is the outcome 1?’, ‘Is the outcome 2?’, ‘Is the outcome 3?’, and ‘Is the outcome 4?’ in a row.
To make things easier to understand, let’s say you roll the die 100 times instead of just once. Since it’s a fair die, you would expect each number to occur 25 times. When the outcome is ‘1’, your friend asks only 1 question. When it is ‘2’, 2 questions. ‘3’ -> 3 questions and ‘4’ -> 4 questions. In total, your friend will have to ask $25 \times (1 + 2 + 3 + 4) = 250$ questions. Therefore, on average, your friend asks $\frac{250}{100} = 2.5$ questions.
You can explore other strategies, but it turns out the optimal strategy is the one that, if possible, keeps asking questions that half the probability of the outcome space. In the above case, your friend can ask, for example,‘Is it below 3?’. If ‘Yes’, he can ask ‘Is it 2?’. If ‘No’, he can ask ‘is it 3?’. Using this strategy, he makes sure that for every outcome, two questions suffice.
Let’s take a look at how many questions on average your friend will ask if he employs this strategy. Again, you roll the die 100 times and each number occurs 25 times. No matter what the outcome is, your friend will always ask two questions, so in total, $100 \times 2 = 200$ questions. On average, 2 questions, which is lower than 2.5 questions.
This, in fact, is the definition of “Bit” and “Entropy”. A question will decreases the level of uncertainty your friend faces. When he employs the optimal strategy, we say that each question decrease his uncertainty by one “bit” and that the entropy of rolling a fair 4-sided die is 2 bits (because on average, it requires at least 2 question to figure out what the outcome is).
Further #
What’s the entropy of rolling an eight-sided fair die? We know that using the optimal strategy, no matter which outcome occurs, your friend only asks 3 questions. So, if you roll 120 times, on average, your friend asks
$$\frac{120 \times 3}{120}$$
3 questions. So the entropy is 3 bits.
The process can be visualized this way:
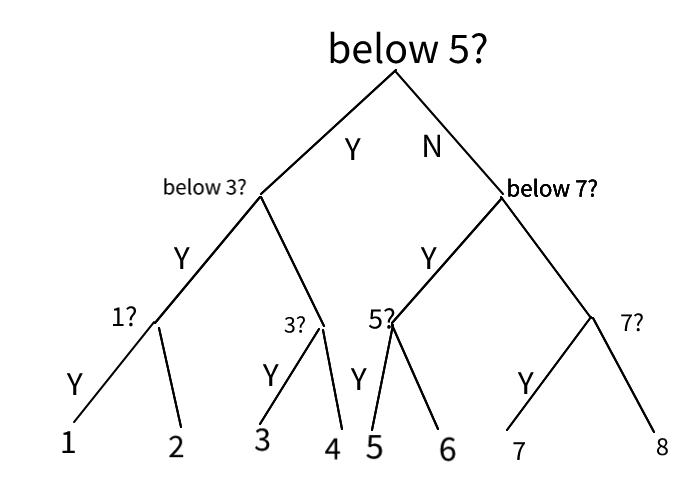
Y: Yes; N: No
The same applies when you roll a 16-sided fair die. Using the optimal strategy, no matter which outcome occurs, your friend will ask 4 questions. The entropy is 4 bits.
It seems if it’s an N-sided fair die, and your friend uses the optimal strategy, no matter which outcome occurs, he will ask $\log_{2}^{N}$ questions. And the entropy of rolling a N-sided fair die is $\log_{2}^{N}$ bits.
Let’s look into why this result. For an N-sided fair die, the probability of each side appearing is $\frac{1}{N}$. No matter which side appears, your friend will ask $log_{2}^{N}$ questions. If we roll the die one time, on average, your friend will have to ask how many questions to figure out the outcome?
$$\sum_{i=1}^{N} \frac{1}{N} \cdot \log_{2}^{N}$$
Non-Uniform Probability distributions #
Above, we only talked about “fair” dies. But what if you have a biased die? Say, each outcome of the four-sided die has these probabilities:
- ‘1’: 1/2
- ‘2’: 1/4
- ‘3’: 1/8
- ‘4’: 1/8
If your friend employs the optimal strategy, which keeps asking questions that half the probabilities, he will ask these questions in a row, until he gets the answer:
- Is it ‘1’?
- Is it ‘2’?
- Is it ‘3’?
Suppose you roll the die once, 1/2 time, the outcome is ‘1’, and your friend will ask 1 question. 1/4 time the outcome is ‘2’, he will ask 2 questions. 1/8 time, the outcome is ‘3’, he asks 3 questions, which is the same for when the outcome is ‘4’.
Therefore, the entropy is:
$$\frac{1}{2}\cdot 1 + \frac{1}{4} \cdot 2 + \frac{1}{8} \cdot 3 + \frac{1}{8} \cdot 3 = 1.75$$
It is clear that the entropy of throwing an N-sided die is this: the sum of the product of each side’s probability times the number of questions required.
Each side’s probability is easy to understand and obtain. But what about the number of questions? It seems that it is related to the probability:
- 1/2 -> 1
- 1/4 -> 2
- 1/8 -> 3
So the number of questions needed for each side (whose probability is $p_i$) is $log_2^{\frac{1}{p_i}}$. Therefore, the entropy of rolling an N-sided die is:
$$\sum_{i=1}^{N} p_i \cdot log_2^{\frac{1}{p_i}} = -\sum_{i=1}^{N} p_i \cdot log_2^{p_i}$$
Comparison #
If you compare the fair 4-sided die and the biased one, you’ll notice that when it’s fair, the probabilities are uniform, and the entropy is the larger (2 bits). When it is biased, the entropy is smaller (1.75 bits).
#MLLast modified on 2025-06-03 • Suggest an edit of this page