Derivatives of 1/x and square root of x

1. $y = \frac{1}{x}$ #

The derivative of $y = \frac{1}{x}$ can be computed in the following way.

First, I highly recommend you to watch this clip , where 3blue1brown visualizes this function.

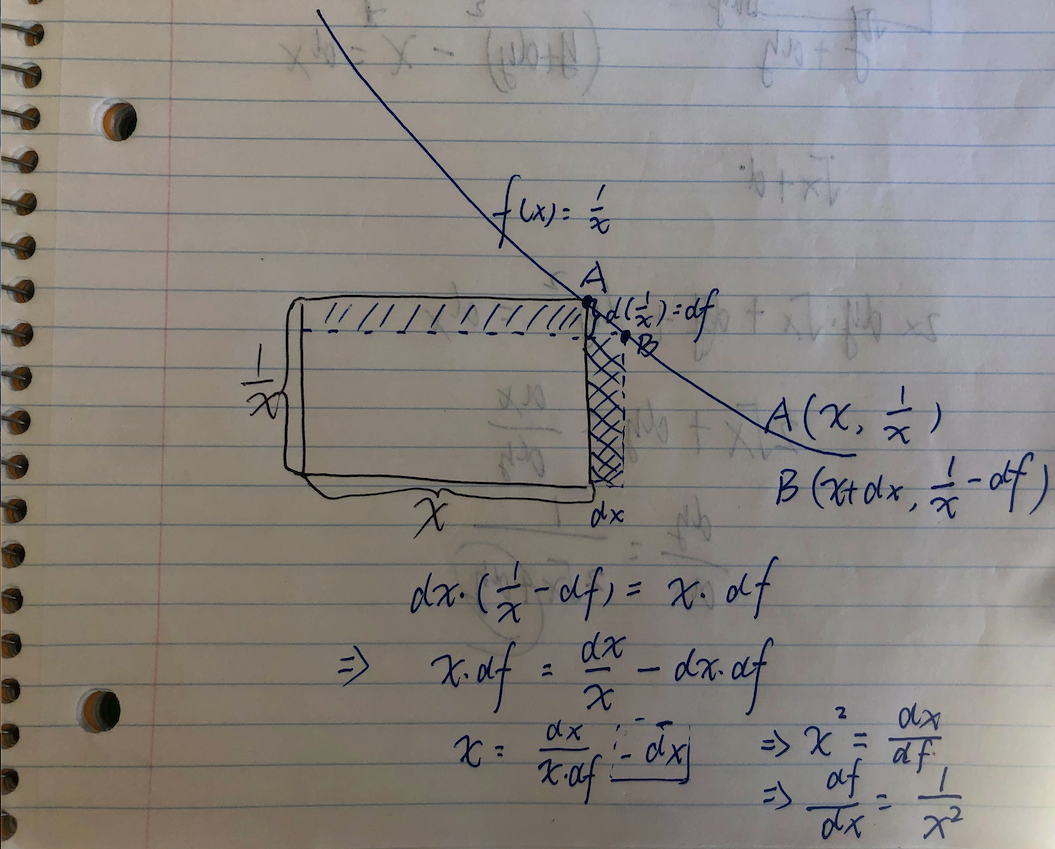
The key part of the proof is that Since A and B are both on the curve of $y = \frac{1}{x}$, the x coordinate times the y coordinate is 1. That is to say: $A_x \cdot A_y = 1$ and $B_x \cdot B_y = 1$. If you know this, then you’ll know that the areas of the two shaded areas are equal. Therefore,

$$dx \cdot (\frac{1}{x} - df) = x \cdot df$$

We have:

$$x\cdot df = \frac{dx}{x} - dx\cdot df$$

So:

$$x = \frac{dx}{x \cdot df} - dx$$

Because $dx$ is extremely small, we can safely ignore it, and therefore, we have:

$$x = \frac{dx}{x \cdot df}$$

Multiply the above equation by $x$ and we have:

$$x^2 = \frac{dx}{df}$$

So we have:

$$\frac{df}{dx} = \frac{1}{x^2} = x^{-2}$$

Because $df$ is negative, the derivative should be negative as well, so:

$$\frac{df}{dx} = - \frac{1}{x^2} = - x^{-2}$$

This method is inspired by F J .

2. $y = \sqrt{x}$ #

It can be proven in two ways.

Intuitive way #

First, let’s use the way suggested by 3blue1brown.

I’ll write $d\sqrt{x}$ as $dy$.

We have

$$dx = 2\sqrt{x}\cdot dy + (dy)^2$$

Divide the equation by $dy$ and we have:

$$2\sqrt{x} + dy = \frac{dx}{dy}$$

Therefore,

$$\frac{dy}{dx} = \frac{1}{2\sqrt{x} + dy}$$

Because $dy$ is approaching zero, we can safely ignore it and we have

$$\frac{dy}{dx} = \frac{1}{2\sqrt{x}} = \frac{1}{2}x^{-\frac{1}{2}}$$

Chain rule #

Let’s say we have $f(x) = \sqrt{x}$, $g(x) = x^2$, and $h(x) = g(f(x)) = (\sqrt{x})^2 = x$.

We have:

$$\begin{align} h^\prime(x) & = 1 = g^\prime(f(x)) \cdot f^\prime(x)\\ & = 2\cdot f(x) \cdot f^\prime(x) \\ & = 2\sqrt{x} \cdot f^\prime(x) \\ \end{align}$$

So we have

$$f^\prime(x) = \frac{1}{2\sqrt{x}}$$

The method by chain rule is inspired by Yifan Wei.

#ML

Last modified on 2025-04-26