Suppose we have:
$$\vec{a} = \begin{bmatrix} a_x \\ a_y \end{bmatrix}$$
$$\vec{b} = \begin{bmatrix} b_x \\ b_y \end{bmatrix}$$
I am wondering why $\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y$.
Let’s prove this by having a concrete example:
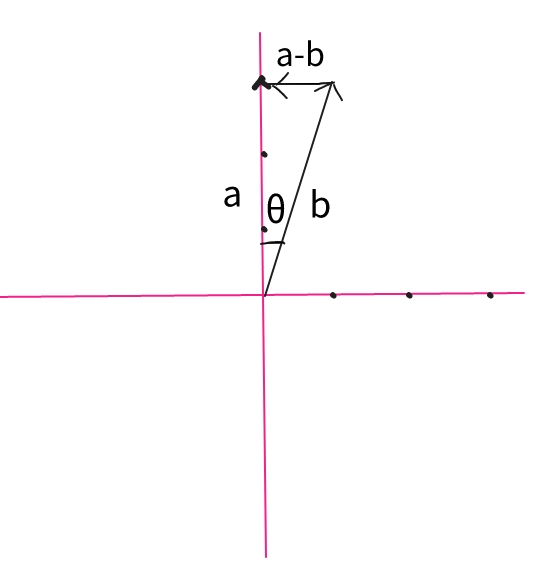
$$\vec{a} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}$$
$$\vec{b} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}$$
If you are familiar with linear algebra, you’ll know that
$$\vec{a}\cdot \vec{b} = ||\vec{a}||\cdot ||\vec{b}|| \cdot \cos \theta$$
If you don’t know why, read here .
We have:
-
$||\vec{a}|| = 3$ -
$||\vec{b}|| = \sqrt{10}$ -
$\cos \theta = \frac{3}{\sqrt{10}}$
Therefore, we have:
$$\vec{a}\cdot \vec{b} = ||\vec{a}||\cdot ||\vec{b}|| \cdot \cos \theta = 3 \times \sqrt{10} \times \frac{3}{\sqrt{10}} = 9$$
Given that
$$\vec{a} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}$$
$$\vec{a} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}$$
We can conclude that
$$\vec{a} \cdot \vec{b} = a_x b_x + a_y b_y$$.
Last modified on 2022-08-27