缘起 #
1921 年 5 月 12 日,我在英格兰的一家农场散步。农场主听说我是一名科学家,向我讨论起他正在选择化肥的难题。他的农场种了 12 公顷的玉米,使用了四家不同化肥公司的产品,今年刚刚丰收,但他却不知道这些化肥是否真的有效。
我被这一问题迷住了。我们自然可以使用 T 检验,对每一种可能的产品对进行对比,但这种方法比较慢。如果农场主只是想知道这四种不同化肥是否效用相同,那是否有更快的方法?
我自然开始用我的拿手好戏:假设检验。如果四种化肥效用相同,结果会怎样?
如果化肥效用相同,则可视为我们从一个总体中随机抽取了四份样本。针对这四份样本,我们有以下几个误差:
- 四个样本各自的均值与样本总均值的误差
- 各自样本内部,每个数据点与各自所在样本的均值之间的误差。
用 $N$ 表示数据总量,$K$ 表示有多少种不同样本,在这里是 4。
$N_i$ 表示第 $i$ 个样本的数据量,$\bar{X}$ 表示所有样本的总均值,$\bar{X_i}$ 表示第 $i$ 个样本的均值,$S^2_i$ 表示第 $i$ 个样本的方差
「四个样本各自的均值与样本总均值的误差」我们记为 SSTrt,计算方法如下:
$$ \text{SSTrt} = \sum_{i=1}^K N_i \cdot \left( \bar{X_i} - \bar{X} \right)^2 $$
「各自样本内部,每个数据点与各自所在样本的均值之间的误差」记为 SSErr,计算方法如下:
$$ \text{SSErr} = \sum_{i=1}^K (N_i - 1) \cdot S^2_i $$
这样求出来的值没办法直接比较,因为 $N$ 与 $K$ 可能不是一个数量级,需要想一个办法求平均值。我们这里除以各自的自由度,而不是直接除以 $N$ 与 $K$,至于为什么,之后再细聊。这样算出来的数我们称为 MSTrt 和 MSErr。
$$ \text{MSTrt} = \frac{\text{SSTrt}}{K-1} $$
$$ \text{MSErr} = \frac{\text{SSErr}}{N-K} $$
最后的重头戏是我们想比较一下这两者,取其商:
$$ F = \frac{\text{MSTrt}}{\text{MSErr}} $$
我回到家,立马用未来世界里的 Python 进行模拟。模拟的方法是这样:一个六面的骰子🎲,随机抛掷一万次,每次记录其面值。然后将此一万个数平均分为四组:
import numpy as np
import pandas as pd
np.random.seed(42)
rolls = np.random.randint(1, 7, size = 10000)
np.random.shuffle(rolls)# Divide rolls into four groups randomly
group_size = len(rolls) // 4
group1 = rolls[:group_size]
group2 = rolls[group_size:2*group_size]
group3 = rolls[2*group_size:3*group_size]
group4 = rolls[3*group_size:]
group_dic = {'A': group1, 'B': group2, 'C': group3, 'D': group4}def calc(group_dic):
res = []
for group, data in group_dic.items():
mu = np.mean(data)
n = len(data)
var = np.var(data, ddof = 1)
res.append({
'treatment': group,
'sample_mean': mu,
'sample_variance': var,
'sample_size': n
})
return res
res = calc(group_dic)
res = pd.DataFrame(res)
res| treatment | sample_mean | sample_variance | sample_size | |
|---|---|---|---|---|
| 0 | A | 3.4796 | 2.977975 | 2500 |
| 1 | B | 3.4692 | 2.952632 | 2500 |
| 2 | C | 3.5276 | 2.843976 | 2500 |
| 3 | D | 3.5232 | 2.905024 | 2500 |
n = res.sample_size.sum()
k = len(group_dic)
n, kgrand_mean = np.sum(
res['sample_mean'] * res['sample_size'])/n
grand_meansstrt = np.sum(
res['sample_size']*(res['sample_mean'] - grand_mean)**2)
sstrtsserr = np.sum(
(res.sample_size -1)*res.sample_variance
)
sserrdftot = n-1
dftrt = k-1
dferr = n-k
mstrt = sstrt/dftrt
mserr = sserr/dferr
mstrt, mserrf_value = mstrt/mserr
f_value一万次悲伤 #
上面我们只是试了一次,让我试一万次,取一万个 $F$,看看分布如何:
def get_group_dic(start, end, size, k):
# Generate random rolls
rolls = np.random.randint(start, end + 1, size=size)
np.random.shuffle(rolls)
# Calculate group size
group_size = len(rolls) // k
remainder = len(rolls) % k # To handle leftover elements
# Create groups dynamically
group_dic = {}
start_idx = 0
for i in range(k):
# Determine the size of the current group
current_group_size = group_size + (1 if i < remainder else 0)
group_dic[chr(65 + i)] = rolls[start_idx:start_idx + current_group_size]
start_idx += current_group_size
return group_dic
def calc_f(group_dic):
res = calc(group_dic)
res = pd.DataFrame(res)
n = res.sample_size.sum()
k = len(group_dic)
grand_mean = np.sum(res['sample_mean'] * res['sample_size'])/n
sstrt = np.sum(res['sample_size']*(res['sample_mean'] - grand_mean)**2)
sserr = np.sum((res.sample_size -1)*res.sample_variance)
dftrt = k-1
dferr = n-k
mstrt = sstrt/dftrt
mserr = sserr/dferr
f_value = mstrt/mserr
return f_valueattempt = 10000
f_values = []
for _ in range(attempt):
group_dic = get_group_dic(1, 7, 10000, 4)
f = calc_f(group_dic)
f_values.append(f)Show Code
import matplotlib.pyplot as plt
# Plot the histogram
plt.figure(figsize=(8, 6))
plt.hist(f_values, bins=50, density=True, alpha=0.75, edgecolor='black', label='Histogram')
# Optional: Add a density line using a kernel density estimate
from scipy.stats import gaussian_kde
density = gaussian_kde(f_values)
x_vals = np.linspace(min(f_values), max(f_values), 1000)
plt.plot(x_vals, density(x_vals), label='Density', linewidth=2)
# Customize the plot
plt.title('Distribution of F Values', fontsize=16)
plt.xlabel('F', fontsize=14)
plt.ylabel('Density', fontsize=14)
plt.legend()
plt.grid(alpha=0.3)
plt.show()
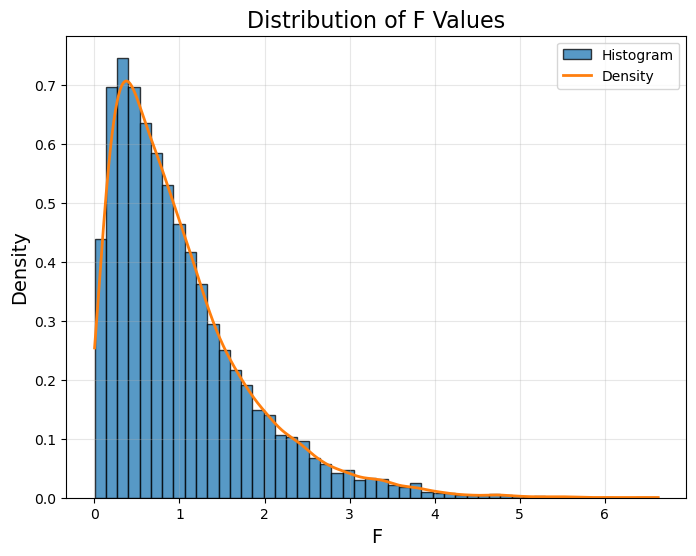
不同的 $N$ 与 $K$ #
设 $N = 3000$,$K = 10$
f_values = []
for _ in range(attempt):
group_dic = get_group_dic(1, 7, 3000, 10)
f = calc_f(group_dic)
f_values.append(f)Show Code
import matplotlib.pyplot as plt
# Plot the histogram
plt.figure(figsize=(8, 6))
plt.hist(f_values, bins=50, density=True, alpha=0.75, edgecolor='black', label='Histogram')
# Optional: Add a density line using a kernel density estimate
from scipy.stats import gaussian_kde
density = gaussian_kde(f_values)
x_vals = np.linspace(min(f_values), max(f_values), 1000)
plt.plot(x_vals, density(x_vals), label='Density', linewidth=2)
# Customize the plot
plt.title('Distribution of F Values', fontsize=16)
plt.xlabel('F', fontsize=14)
plt.ylabel('Density', fontsize=14)
plt.legend()
plt.grid(alpha=0.3)
plt.show()
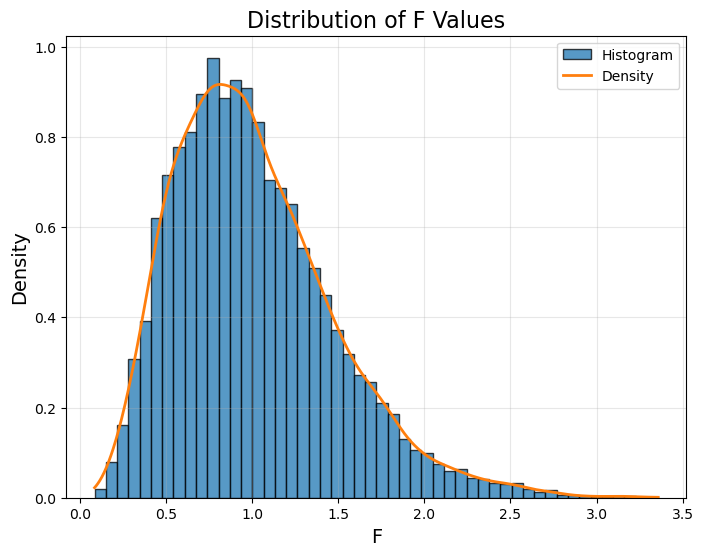
结论与未竟事宜 #
结论就是,如果我们知道 $N$ 与 $K$,那么就可以通过对比上面的图,知道 $H_0: \mu_1 = \mu_2 = ... \mu_K$ 是否成立。
但是有几个点我还没搞清楚:
- 为什么 F 的期望值是 1,因此 F 检验是一个单尾检测?
- 上面的模拟我没有考虑各组样本量不同的情况,如何证明其不影响最后的结果?
- 需要严谨的数学证明来推导出在已知两个既定自由度情况下,F 分布的 PDF 与 CDF 的精确公式。这样就不用每次都模拟,而且更为精确。
这些工作就让我的学生 Ronald Fisher 来完成吧。
#统计最后一次修改于 2025-07-02 • 编辑本页