import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t英文维基百科上的置信区间 (confidence interval) 词条 对此概念解释非常详细。
我们依然拿天狼星人举例子。SpaceX 公司登陆火星之后发现火星地下上全是天狼星人。他们搜集了全部的在火星上居住天狼星人的信息之后,对其进行抽样。随机抽取了 100 个天狼星人,然后测量他们的智商 ($X_1, X_2, X_3, ... X_n$)。记样本均值为 $\bar{X}$、样本方差为 $S^2$。
我们现在最迫切需要知道的是:天狼星人的智商大体是什么样。
注意,我们现在不是要去比较天狼星人和地球人智商有没有显著差异,而是想知道天狼星人的智商大概是什么样。你当然可以直接抛给我一个数:$\bar{X}$,说这是这 100 个天狼星人的平均智商。但是,问题是,我想知道母体的数据啊。
怎么办?
我们把所有天狼星人智商这一母体的均值记为 $\mu$,方差记为 $\sigma^2$。
假设上面的抽样进行无数次,也就是每次随机抽取 100 个天狼星人,记录其样本均值和方差,并且每次算出
$$T = \frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}}$$
其中 $n = 100$。
你会说,等等,$\mu$ 我们并不知道啊,$T$ 根本没法算。
确实,一个具体的 $T$ 在我们不知道母体均值 $\mu$ 的情况下确实没办法计算。但是,回顾一下我们对于 t 分布的讲解
,你会发现,不管母体如何,每次从母体中随机抽取 100 人,计算 $T$ ,重复无数次,这些 $T$ 的分布全部都是 $T \sim t_{99}$:
## params
df = 99
alpha = 0.05
x = np.linspace(-4, 4, 1000)
# calculate PDF for t-distribution
y = t.pdf(x, df=df)
# critical values for the given alpha level
q_value_upper = t.ppf(1 - alpha/2, df)
q_value_lower = t.ppf(alpha/2, df)
# Plot the t-distribution PDF
plt.figure(figsize=(12, 6))
plt.plot(x, y, color='steelblue', lw=2,
label=rf'$t$-distribution with $df={df}$')
# Fill the area between the critical values for the two-tailed region
plt.fill_between(x, y,
where=np.logical_and(x <= q_value_upper, x >= q_value_lower),
color='orange',
alpha = 0.5,
label=rf'Critical Region ($1 - \alpha = {1 - alpha:.2f}$)')
plt.axvline(q_value_lower, color="purple",
linestyle='--',
label=f'Lower Critical Value ({q_value_lower:.2f})')
plt.axvline(q_value_upper, color="red",
linestyle='--',
label=f'Upper Critical Value ({q_value_upper:.2f})')
plt.axhline(0, color = "black")
plt.xlabel(r'$T$', fontsize = 14)
plt.ylabel(r'$P(T)$', fontsize = 14)
plt.title(rf'T-Distribution with {df} Degrees of Freedom', fontsize = 16)
plt.grid(True, linestyle='--', alpha = 0.6)
plt.legend(fontsize = 12)
plt.show()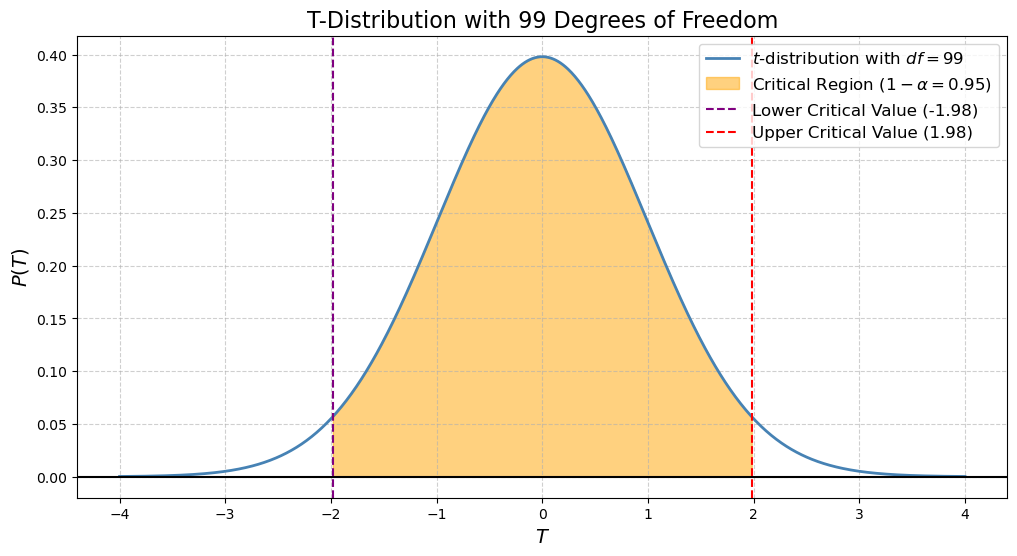
置信区间的构成 #
我们把 $t_{99}$ 的 $97.5\%$ 百分位数 (percentile) 记为 $c$,也就是上图中红线所对应的 $T = 1.98$。其所代表的含义是所有的 $T$ 中,落在红线以及红线往左这个区域的 $T$ 占比为 $97.5\%$。也可以理解为,随机一个 $T$ 落在红线以及红线往左这个区域的概率是 $97.5\%$
因为 $t$ 分布是对称的,所以一个随机的 $T$ 落在 $[-c, c]$ 这个区间 (也就是上图的黄色区域所对应的 $T$ 值区间) 的概率是 $95\%$,我们可以表示为:
$$P_T (-c \le T \le c) = 0.95$$
代入上面的 $T$ 计算公式可得到:
$$P (-c \le \frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \le c) = 0.95$$
所以
$$P (-c \cdot \frac{S}{\sqrt{n}} \le \bar{X} - \mu \le c \cdot \frac{S}{\sqrt{n}}) = 0.95$$
所以
$$P (-c \cdot \frac{S}{\sqrt{n}} - \bar{X} \le - \mu \le c \cdot \frac{S}{\sqrt{n}} - \bar{X}) = 0.95$$
所以
$$P_{\mu} (\bar{X} - \frac{c \cdot S}{\sqrt{n}} \le \mu \le \bar{X} + \frac{c \cdot S}{\sqrt{n}})$$
我们把
$$\left[\bar{X} - \frac{c \cdot S}{\sqrt{n}}, \bar{X} + \frac{c \cdot S}{\sqrt{n}} \right]$$
称为母体均值 $\mu$ 的 $95\%$ 置信区间。
我们也可以这样记:$\mu$ 的 $1 - \alpha$ 置信区间为:
$$P_{\mu} (\bar{X} - \frac{S}{\sqrt{n}} \cdot t_{n-1, \frac{\alpha}{2}} \le \mu \le \bar{X} + \frac{S}{\sqrt{n}} \cdot t_{n-1, 1- \frac{\alpha}{2}})$$
置信区间的解读 #
也许很多人将
$$P_{\mu} (\bar{X} - \frac{c \cdot S}{\sqrt{n}} \le \mu \le \bar{X} + \frac{c \cdot S}{\sqrt{n}})$$
或者
$$\left[\bar{X} - \frac{c \cdot S}{\sqrt{n}}, \bar{X} + \frac{c \cdot S}{\sqrt{n}} \right]$$
错误地理解为:
母体均值
$\mu$落在以上区间的概率是 95%。
这一解读之所以错误是因为虽然 $\mu$ 未知,但却是一个具体的值 (「常量」),而不是一个变量。当一个样本被观测到之后,$c, S, n, \bar{X}$ 这些全都是常量,以上的区间也是一个常量。所以 「$\mu$ 在这个区间」并不存在概率一说。它要么在,要么不在。
既然
$$P_{\mu} (\bar{X} - \frac{c \cdot S}{\sqrt{n}} \le \mu \le \bar{X} + \frac{c \cdot S}{\sqrt{n}})$$
的确是一个概率,但是 $\mu$ 是一个常量,那变量只能是这个区间了。所以置信区间正确的理解为:
从一个分布为 $\mathcal N \sim(\mu, \sigma^2)$ 的母体中随机一个大小为 $n$ 的样本,算出 $\bar{X}$ 和 $S$,记 $b$ 为 $t_{n-1}$ 这一分布的 $\frac{\alpha}{2}$ 百分位数 (percentile),$c$ 为 $t_{n-1}$ 这一分布的 $1 - \frac{\alpha}{2}$ 百分位数 (percentile),并计算出这样一个区间
$$\left[\bar{X} + \frac{b \cdot S}{\sqrt{n}}, \bar{X} + \frac{c \cdot S}{\sqrt{n}} \right]$$
上面这个过程我们重复无数次,得到无数个这样的区间。那这些区间中,有 $\left( 100 (1 - \alpha) \right) \%$ 包含了母体均值 $\mu$。
上面这个公式我换成了 $b$ 和 $c$,而不是 $-c$ 和 $c$ 是因为不是所有的分布都对称,比如卡方分布
。
置信区间和假设检验的关系 #
我们随机抽取了 100 个天狼星人,算出了样本均值$\bar{X}$、样本标准差 $S$,并由此构造了一个 $95\%$的置信区间。
假如上帝将天狼星人智商这一母体的均值 $\mu$ 告诉我们了,而且我们看到这一均值就在这个置信区间之内。那么,我们也可以知道,用这个样本数据算出的 $T$,一定落在上图的黄色区域。
为什么呢?
因为
假如上帝将天狼星人智商这一母体的均值
$\mu$告诉我们了,而且我们看到这一均值就在这个置信区间之内
意味着
$$\bar{X} - \frac{c \cdot S}{\sqrt{n}} \le \mu \le \bar{X} + \frac{c \cdot S}{\sqrt{n}}$$
成立。所以
$$-c \cdot \frac{S}{\sqrt{n}} \le \bar{X} - \mu \le c \cdot \frac{S}{\sqrt{n}}$$
成立。所以
$$-c \le T = \frac{\bar{X} - \mu}{\frac{S}{\sqrt{n}}} \le c$$
成立。
所以「用这个样本数据算出的 $T$,一定落在上图的黄色区域」。
模拟 #
我比较懒,有一个现成的模拟置信区间构成过程的网站:https://www.rossmanchance.com/applets/2021/confsim/ConfSim.html 。我目前就懒得重新弄了。
其中 Describe process 的选择:
Statistics: Means
Distribution: Normal
Method: t
Population mean: 3
Population SD: 10.0
Sample size: 100
Number of intervals: 100
其他不用动,然后点击 Sample 这个按钮。
最后一次修改于 2025-07-02 • 编辑本页