using Plots
微分 #
假设有如下的情况。横坐标表示时间,纵坐标表示一辆车从 t = 0 开始所走过的路程。比如,在 t = 2 时,行使的路程大概是 6.5,在 t = 5 时,路程大概是 21.5。
g(x) = - 1/3 * x^3 + 2.5x^2
plot(g, 0, 5,
label="",
xlabel = "Time (s)",
ylabel = "Distance (m)",
linewidth=3
)
savefig("/cn/blog/2023-02-26-intro-to-calculus_files/calculus-01.png")
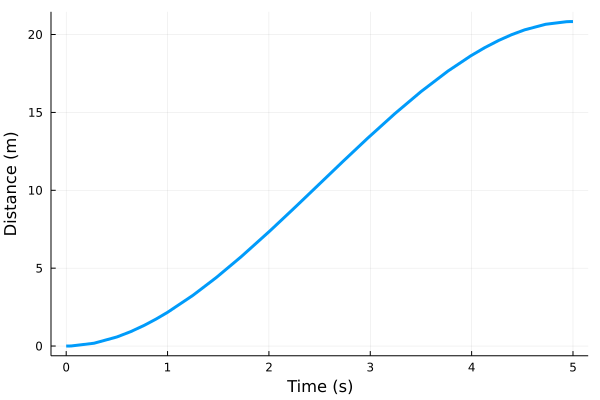
图一
如果我现在问你,该车辆在每一个时间点的速度为何,你如何解决。比如,在 t = 2 时的速度。
我们一般对「速度」的解读是:一秒跑多少米。但是,需要注意的是,我们在考察速度时,并不是限定在一秒这个时间里,而是在某一个非常小的时间点。比如,我们会指着一辆飞奔的车,说,这车开得好快。我们这样说时,是指我们看它的那一瞬间它的速度很快,而不是说从我们看它开始接下来一秒之内很快(这车接下来一秒会怎样,我们并不知道)。理解了这个,你就知道速度是对于某一个非常小的时间段来说的。
回到 t = 2 时的速度。我们可以这样看,比如,我在 2 秒上加非常小,非常非常小的一个时间,$\Delta t$。上面那个距离相对于时间的方程式我们表示为 $s(t)$:
$$s(t) = - \frac{1}{3} x^{3} + \frac{5}{2} x^2 $$
那么,该车辆在 2s 时的速度为:
$$\begin{aligned} v(t = 2) & = \frac{s(2 + \Delta t) - s(2)}{\Delta t} \\ & = \frac{- \frac{1}{3} (2 + \Delta t)^{3} + \frac{5}{2} (2 + \Delta t)^2 + \frac{1}{3} 2^{3} - \frac{5}{2} 2^2}{\Delta t}\\ & = \frac{-\frac{1}{3}\Delta t^3 +6 \Delta t + \frac{1}{2} \Delta t^2}{\Delta t} \\ & = -\frac{1}{3}\Delta t^2 + \frac{1}{2} \Delta t + 6 \end{aligned}$$
因为 $\Delta t$ 非常非常小,我们可以忽略 $-\frac{1}{3}\Delta t^2 + \frac{1}{2} \Delta t$,所以 $v(t = 2) = 6$。带入 $x = 0.01$,我们看一下:
(g(2 + 0.01) - g(2))/0.01
6.004966666666434
更普遍一点,我们想一下,回到刚才的问题,这辆车在 $x$ 秒时的速度为多少?
$$\begin{aligned} v(t = x) & = \frac{s(x + \Delta t) - s(x)}{\Delta t} \\ & = \frac{- \frac{1}{3} (x + \Delta t)^{3} + \frac{5}{2} (x + \Delta t)^2 + \frac{1}{3} x^{3} - \frac{5}{2} x^2}{\Delta t}\\ & = \frac{- x^2\Delta t - x \Delta t^2 - \frac{1}{3}\Delta t^3 + 5x \Delta t + \frac{5}{2} \Delta t^2}{\Delta t} \\ & = - x^2 - x \Delta t - \frac{1}{3} \Delta t^2 + 5x + \frac{2}{5} \Delta t \end{aligned}$$
因为 $\Delta t$ 很小,可以忽略,那上面的式子就简化为:$- x^2 + 5x$。这就是 $s(t) = - \frac{1}{3} x^{3} + \frac{5}{2} x^2 $ 的 微分方程,可以写成
$$s^\prime(x) = - x^2 + 5x$$
也就是:
f(x) = - x^2 + 5x
plot(f, 0, 5,
label="",
xlabel="Time (in seconds)",
ylabel="Speed ",
linewidth=3
)
savefig("/cn/blog/2023-02-26-intro-to-calculus_files/calculus-02.png")
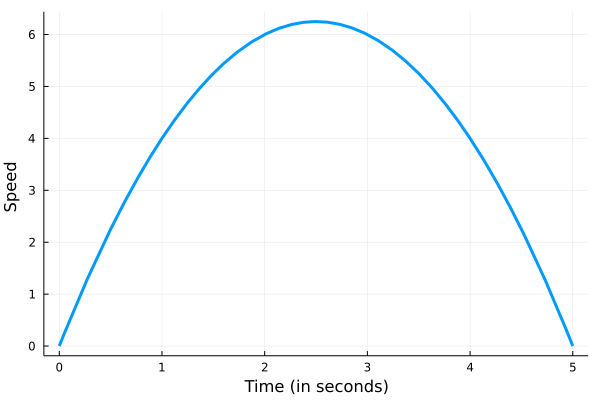
图二
带入 $x =2$,我们得到 $s^\prime(2) = - 2^2 + 5\cdot 2 = 6$。和上面的结果一样。
积分 #
好,说完微分,我们来看一下积分。就拿上面那个图来说,也就是速度那张图。现在,假设我们不知道该车辆行驶路程相对于时间的方程式,只知道该车之速度相对于时间的方程式为
$$f(x) = x (5 - x)$$
根据这个,你能告诉我,该车辆行驶路程相对于时间的方程式 $g(x)$ 是什么吗?
上面这个比较难,那我们可以想象一下,如果该车行驶速度相对于时间的关系为:
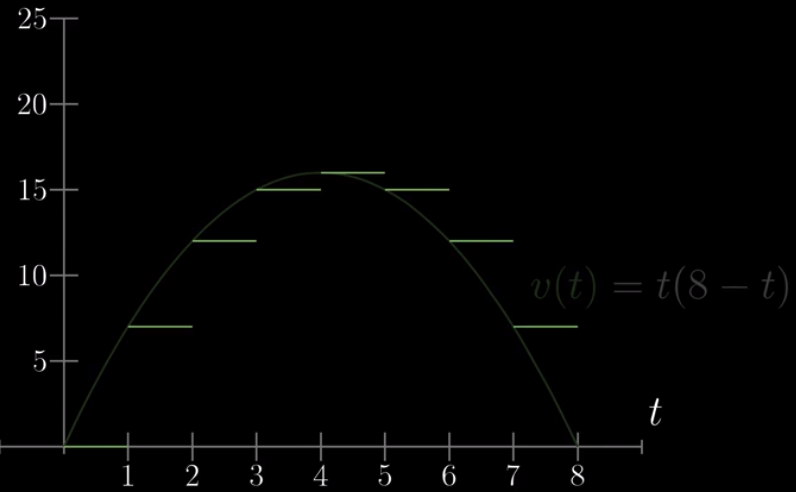
那路程如何计算就很好理解了,就单纯时间乘以速度,把所有的加起来就可以了
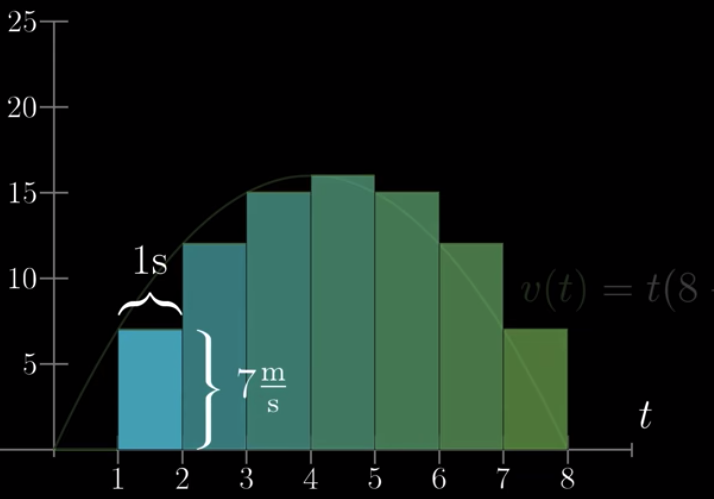
上面的每段时间如果越来越短,越来越短,就是这样的结果
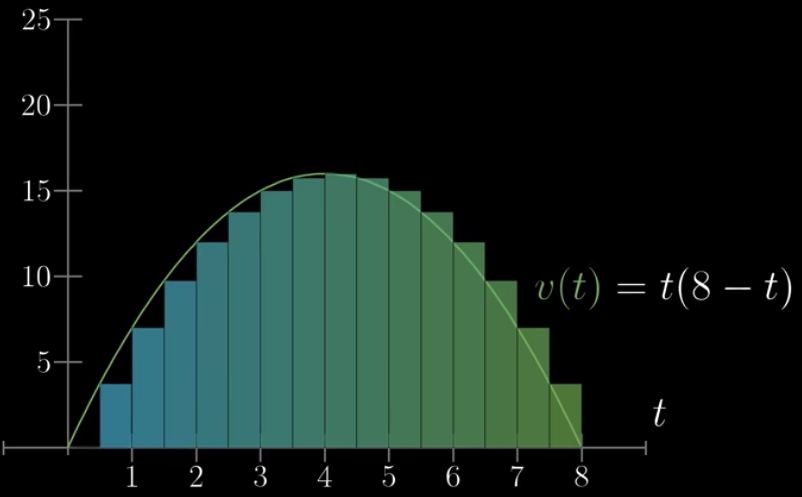
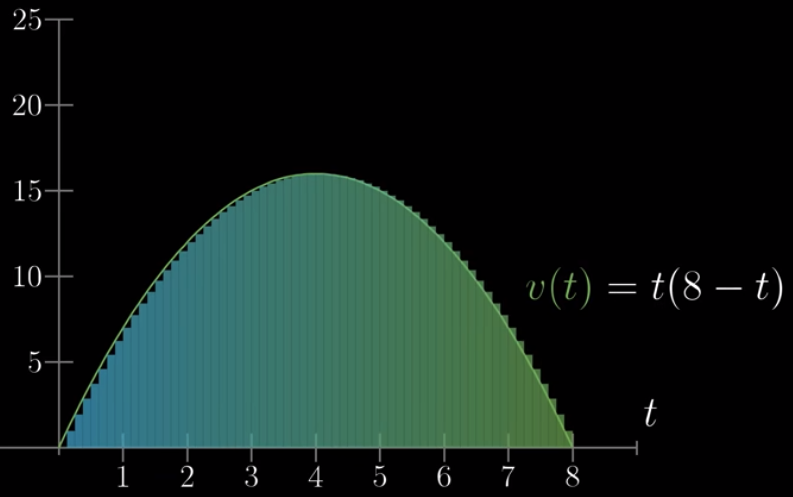
如果你可以理解上面的内容,那么你就知道,该车辆在某一时间点,比如 $t = 2$,行驶过的距离,就是从 $t=0$ 到 $t=2$ 这段在图二中的面积。
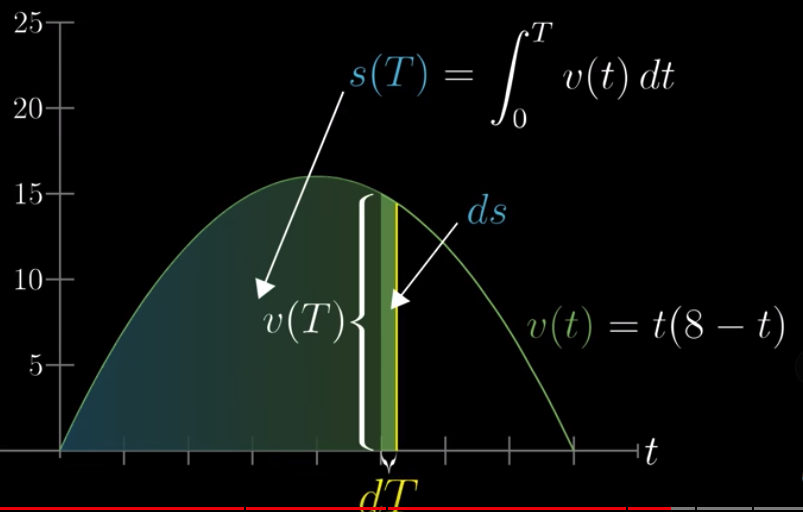
如上图所示。如果我们用 $s(T)$来表示路程与时间的关系。假设我们有一个非常小的时间,$dT$,带来的是路程增加了 $ds$。$ds$ 就相当于那个标亮小矩形的面积。该面积在 $dT$ 非常小时可以用 $dT * v(T)$ 来近似。所以我们有:
$$\frac{ds}{dT} = v(T)$$
根据微分的定义,我们可以知道 $v(T)$ 是 $s(T)$ 的导数。那什么样的函数其导数为 $f(x) = -x^2 + 5x$ 呢?应该是
$$g(x) = -\frac{1}{3}x^3 + \frac{5}{2}x^2 + c$$
其中 $c$ 是一个常数。因为 $g(0) = 0$ (在时间为 0 时,所行驶过的路程为 0),所以 $c = 0$。所以
$$g(x) = -\frac{1}{3}x^3 + \frac{5}{2}x^2$$
这有什么意义呢?意义非常大。你换一个思路看,如果一上来就问你,在图二的函数中,从 $f(0)$ 到 $f(x)$ 这段的面积和 $x$ 是什么函数关系,比如,我想知道从从 $f(0)$ 到 $f(4)$ 这段的面积是什么,你是不是一上来根本不知道怎么解决?但理解了积分之后,你就知道,那段的面积与自变量的关系就是该函数的积分方程。这样就很好解决了。
最后一次修改于 2023-02-26