上篇,也就是第二章,k老师主要是简单介绍了一下贝叶斯的方法。第三章是介绍了 r 语言的基本操作,这里不再介绍。从第四章开始,整本书渐渐进入主体,开始涉及贝叶斯的核心。
第四章开始讲概率 (probability)。概率是用来描述不确定性 (uncertainty) 的。假如我现在抛一枚硬币,掉下来之后有可能是正面朝上,也可能是背面朝上。每当我们讨论一种结果的可能性的时候,我们其实在头脑里想到了所有可能的结果,这些所有可能的结果叫做样本空间 (sample space)。
如果这个硬币质地良好,那么正面朝上的概率是 50%。如果质地粗糙,那么正面朝上的概率有可能大于50%,也可能小于50%。我们用希腊字母 θ 来表示正面朝上的概率。如果 $\theta = 50\%$ ,那说明硬币质地良好。
另一个层面,我们对于 $\theta$ 的值其实也是有预设的。如果这枚硬币是国家铸币厂生产的,那么 θ=50% 的概率会很高,如 $p(\theta = 0.5)=0.99$, 如果这枚硬币是小作坊生产的,那么 $p(\theta = 0.5)$ 可能只有0.01.
回到样本空间这个概念。抛一枚硬币这个事件的样本空间有2种可能的结果:正面朝上、背面朝上。猜测硬币的质地时,样本空间有无数种可能的结果:从 $\theta =0.0$ 到 $\theta =1.0$ 之间所有的数字都有可能。
你可能像我一样对掷硬币已经不耐烦了,因为已经在太多教材中看过。但是k教授说到,掷硬币可以用来代表几乎所有二元性的事件:选a还是选b、药物有效还是无效、正确还是错误等等。所以我们还是要研究掷硬币。
当我们说,一个质地良好的硬币,正面朝上的概率是50%时,我们是说,将这个硬币抛掷无数次,有50%的次数是正面朝上的。也就是说,这个概率是指,从长远来看的相对频率。
有两种方法来获取这个从长远来看的相对频率:
- 模拟;
- 数学公式推导
第一种方法,模拟。我们用 R 语言来模拟。假设计算机预算 $\theta = 0.8$,也就是正面朝上的概率是 80%,但是我们不知道。我们只能通过观察计算机的掷币结果来推测。
下面我们在计算机上模拟抛掷一枚 $\theta = 0.8$ 的硬币一万次。代码1如下:
n <- 10000
pheads <- 0.8
flips<-sample (x=c(0,1),prob=c(1-pheads, pheads),size=n, replace=TRUE)
num.heads <- cumsum(flips)
total.toss <- c(1:n)
prob.heads <- num.heads / total.toss
plot (total.toss, prob.heads, type = 'o', log='x',
col="skyblue",cex.axis = 1.5,
xlab = "Flip Number", ylab = "Proportion Heads", cex.lab = 1.5,
main = "Running Proportion of Heads", cex.main=1.5)
abline( h=pheads, lty="dotted")
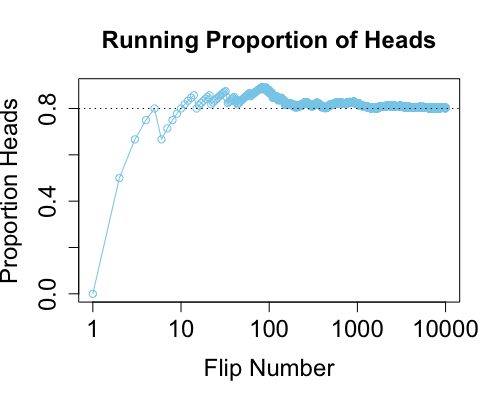
图4.0, 抛一万次硬币猜正面朝上的概率
我们会看到,抛掷一万次,正面朝上的频率越来越接近0.8,那么我们在不知道 $\theta = 0.8$ 的情况下,看到这个结果,自然也就会猜到 $\theta = 0.8$。
第二种方法是数学公式推导。比如有一个六面的骰子🎲,画了一个点的有一个面,两个点的有两个面,三个点的有三个面,那么用数学公式我们可以得出,抛掷骰子后,从长远来看,得到一个点的相对频率是1/6,两个点1/3,三个点1/2.
概率分布 #
所谓概率分布,是指列出所有可能的结果及它们各自的对应的概率。Kruschke 老师的原话是:
A probability distribution is simply a list of all possible outcomes and their corresponding probabilities (p.78).
谈到概率分布 (probability distribution) 的时候,首先需要区分这个变量是离散的 (discrete) 的还是连续的 (continuous)。离散型变量很好理解,比如抛硬币,就只有两种结果2,正面朝上和反面朝上。连续型变量比较复杂。
对于连续型变量而言,某一个具体的值的概率是无限接近于0的。比如,我们随机抽取全部中国人的身高,画成一个身高分布图,那么一个人身高非常精确得为1.789054890234……的概率3是多少?是一个无限接近于零的数字。也就是说,对于一个连续型变量,比如身高,谈论一个具体值的概率3是没有意义的。
那么,对于连续型变量,我们就没办法谈论概率了吗?当然不是。有两种办法让我们可以研究连续型变量的概率:
- 概率质量 (probability mass)
- 概率密度 (probability density)
所谓概率质量,是把所有可能的结果分成无数个互斥并穷尽 (mutually exlusive and exhaustive) 的区间 (intervals),然后看结果落在某一区间的频率,即为概率,也就是这个结果的概率质量。

图4.2-1

图4.2-2, 来源: Kruschke 老师的教材 p.79
上图中,k 教授举的例子 是身高,不过单位是英尺。我就不解释了。图示很容易看懂。注意,这两个图看分子,即: prob.mass,先不要看分母,因为考虑分母的话,prob.mass / bin width 就是概率密度了。
用概率质量有一个不足:区间的宽度很随意,可宽可窄。因此,为了更准确地讨论连续性变量的概率,我们可以考虑第二种方法,即:概率密度。我们把区间设成无限窄。然后,我们不去看这个无限窄区间的概率质量,而是看概率质量与区间宽度的比例。这个比例便是概率密度。
回到图4.2。prob.mass / bin with 即为 概率质量 / 区间宽度,结果是概率密度。图4.2-1的区间宽度为2.0个单位,4.2-2的区间宽度为1.0个单位。我们当然可以将这区间宽度进一步减小,如:

图4.3, 来源: Kruschke 老师的教材 p.81
这个例子中,区间宽度是0.25个单位。我们看到,虽然概率质量不可能大于14,但概率密度是有可能大于1的,特别是当区间宽度非常小的时候。
概率质量有一个特征是,所有概率质量加起来等于1。这个应该很好理解。因为概率质量的公式中,分母是样本总量,分子是落在这个区间的样本量,那么所有区间的概率质量相加的话,分母不变,分子是所有区间的样本总量相加,结果是:总共的样本量。分子分母相等,商自然等于1。用数学公式表达的话:
$$\sum_i p([x_i,x_i + \Delta x]) = 1 \tag{4.1}\label{eq4.1}$$
这个公式里,$x_i$ 可以理解成从做到右第几根竖线,比如,图4.3,第二根竖线就是正好 83.6 那里。$\Delta x$ 表示区间宽度。那么 $[x_i,x_i + \Delta x]$ 表示的是第 $i$ 个区间 (interval),例如,$[x_1,x_1 + \Delta x]$ 表示第 1 个区间。
那么概率密度呢?
根据概率密度的定义(概率质量除以区间宽度),$x$ 变量上的概率密度可表示为:
$$\frac{p([x_i,x_i + \Delta x])}{\Delta x}$$
结合公式 $\eqref{eq4.1}$, 可知:
$$\sum_i \Delta x \frac{p([x_i,x_i + \Delta x])}{\Delta x} = 1 \tag{4.2}\label{eq4.2}$$
当区间宽度变得无限小 (infinitesimal),我们用 $d(x)$ 取代 $\Delta x$ 来表示区间宽度。另外,我们用 $p(x)$ 来表示 $x$ 变量的概率密度,则有:
$$\int d(x)p(x) = 1\tag{4.3}\label{eq4.3}$$
这里值得指出的是,$p(x)$,也就是 $x$ 的密度函数,在不同的情况下是有不同的具体公式的,比如,我们来看最著名的正态分布:

图4.4, 来源: Kruschke 老师的教材 p.83
正态分布中,概率密度函数的数学公式为:
$$p(x) = \frac{1}{\sigma \sqrt{2 \pi}} exp \left(-\frac{1}{2}\left[\frac{x-\mu}{\sigma}\right]^2\right)\tag{4.4}\label{eq4.4}$$
这里有一个点需要特别注意:对于连续型变量,任何一个具体值的概率质量都无限接近于零,但是,任何一个具体值的概率密度则是有具体的值的。比如,在图 4.4 所示的正态分布中,$p(-0.2) \approx 1.15$
Kruschke 教授之后在 4.3.3 章节从纯数学(涉及到微积分)角度探讨了平均数和标准差,这部分我还没能力看懂,不过没关系,这部分可以之后再看,不影响随后的理解。
虽然如此,我还是想把 K 老师讲到的期望值,也即平均值,这部分简单提一下。
K 老师讲到,当 $x$ 是离散型变量时,这个分布的期望值可以表述为:
$$E[x] = \sum_x p(x) x \tag{4.5}\label{eq4.5}$$
其中,$p(x)$ 在这里是代表概率质量,因为这是离散型变量。
上面这个公式应该很好理解。举个例子:比如我们抽奖,抽中100元的概率是0.001,抽中50元的概率是0.01,抽中10元的概率是0.05,抽中1元的概率是0.1,剩下的概率,即 $1-0.001-0.01-0.05-0.1 = 0.839$, 是我们什么奖都抽不到。那么我们抽一次奖,平均而言,能抽中多少钱呢?所谓“平均而言”,可以理解成如果无数次抽奖,平均得到多少钱?很简单:
\begin{align} E[x] & = 100\times0.001+50\times0.01+10\times0.05+1\times0.1+0\times0.839 \\ & = 0.1+0.5+0.5+0.1+0 \\ & = 1.2 \end{align}
也就是说,我们平均能抽中1块2。如果抽一次奖需要两块钱,那显然商家是赚的(那肯定啊…赔本的买卖谁做啊)。
那如果 $x$ 是连续性变量呢?
$$E[x] = \int dx \ p(x) x \tag{4.6}\label{eq4.6}$$
这里 $p(x)$ 是概率密度,那 $dx \ p(x)$便可以理解成区间无穷小的概率质量。上面这个公式应该不难理解。
最高密度区间 (HDI) #
描述一个分布,除了可以说明平均数和标准差,另一个重要方法是最高密度区间 (highest density interval; HDI)。HDI 首先是区间,这个区间有什么特征呢:这个区间所有点的概率密度大于这个区间外的点。
对于 HDI,有两个需要注意的点:
- HDI 不一定非要左右对称;
- HDI 不一定是连续的。

图4.5, 来源: Kruschke 老师的教材 p.88
HDI 越宽,说明我们越不确定;越窄说明越确定。
边缘分布和条件分布 #
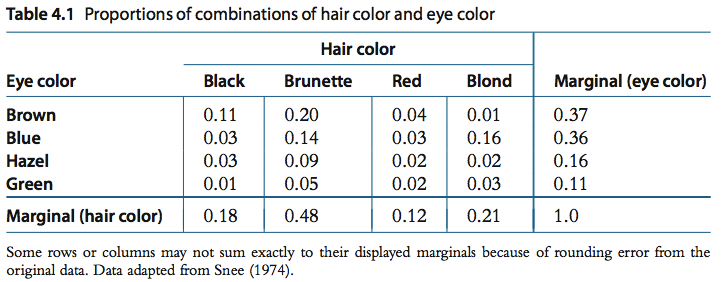
表4.0, 来源: Kruschke 老师的教材 p.90
这个表的数据来自 R 自带的 HairEyeColor。行代表“眼睛颜色”,列代表“头发颜色”。边缘概率分别在最右和最底。每一个单元格中的数据是”组合概率“(joint probability)。比如,(black hair, brown eye) 这个单元格的概率是 0.11,也就是说一共有 11% 的人是黑头发、褐眼睛。同理,黑头发、蓝眼睛的概率只有 3% 。我们把这里的组合概率记为 $p(e,h)$ 或者,$p(h,e)$,很明显 $p(e,h) = p(h,e)$ 。
有时候我们只对某一个眼睛颜色,或者头发颜色作为整体感兴趣。比如,我们想知道有多少人是蓝色眼睛,有多少人是红色头发,有多少人是金黄色头发,等等。这种即为“边缘概率” 。只需要把每一行、每一列单独求和即可。比如,褐色 (brown) 眼睛这一行:
$$.11 + .20 + .04 + .01 = .37$$
再比如,黑色 (black) 头发这一列:
$$.11 + .03 + .03 + .01 = .18$$
如果是看眼睛的话,我们把边缘概率标记为 $p(e)$ ,同理头发的边缘概率是 $p(h)$。这里需要注意的是,这里的 $e$ 和 $h$ 是统称。具体的话,如$p(e_{black})$、$p(h_{blond})$。
解释了“组合概率” 和“边缘概率”, 我们来看一下和贝叶斯统计密切相关的“条件概率” 。所谓条件概率,是指在某个条件下,求一个事件的概率。比如,回到表 4.0, 我告诉你一个人的头发颜色是黑色,那么他/她的眼睛是蓝色的概率是多少?你可以想象一下,有一个木板在把一个人的头部全部挡住,我现在缓慢将木板下移,漏出这个人的头发,是黑色的。我现在问你,这个人的眼睛是蓝色的概率是多少?
有人说是 0.03, 因为 $p(h_{black} , e_{blue}) = 0.03$。错。为什么错?因为没有考虑到已知的条件。
我们回到表 4.0。我们假设一共有100个人,那么既有黑色头发又有蓝色眼睛的一共有 3 个人。好,现在已知这个人头发是黑色的,问你他/她眼睛是蓝色的概率,你如果答 0.03 的话,分母是什么?是总共的 100 个人。但是,我既然已经告诉你这个人头发是黑色了,这个信息你用到了吗?
因为头发是黑色的一共有 18 个人,这 18 个人中,有 3 个人的眼睛是蓝色的,那么概率自然是 3/18 = 1/6。这里,你能发现什么?
$条件概率 = 组合概率 / 边缘概率$
即:
$$p(e|h) = p(e,h)/p(h)$$
这里,$p(e|h)$ 表示 “已知 h,求 e 的概率”。
回到刚才的例子。我们知道这个人的头发是黑色的,那么我们就把目光聚焦在 “hair color : black” 这一列,别的列都不去管。组合概率(黑色头发并且蓝色眼睛)为 0.03,也即 $p(h_{black} , e_{blue}) = 0.03$,边缘概率为 0.18,也即 $p(h_{black}) = 0.18$。那么条件概率为 0.03/0.18 = 1/6 。
我们来考虑更一般的情况:
| * | * | hair | * | sum | |
|---|---|---|---|---|---|
| Eye | 1 | 2 | 3 | 4 | |
| A | n | ||||
| B | |||||
| C | |||||
| D | |||||
| sum | m | z |
如果 n , m , z 是具体的人数,而非比例,那么
最后一次修改于 2022-06-18